引言

为什么写这本书？关于 Swift，已经有大量来自 Apple 的现成文档，而且还有更多的书正在编写中。为什么世界上依然需要关于这种编程语言的另一本书呢？

这本书尝试让你学会以函数式的方式进行思考。我们认为 Swift 有着合适的语言特性来适配函数式的编程方法。然而是什么使得程序具有函数式特性？又为何要一开始就学习关于函数式的内容呢？

很难给出函数式的准确定义 — 其实同样地，我们也很难给出面向对象编程，亦或是其它编程范式的准确定义。因此，我们会尽量把重点放在我们认为设计良好的 Swift 函数式程序应该具有的一些特质上：

• 模块化： 相较于把程序认为是一系列赋值和方法调用，函数式开发者更倾向于强调每个程序都能够被反复分解为越来越小的模块单元，而所有这些块可以通过函数装配起来，以定义一个完整的程序。当然，只有当我们能够避免在两个独立组件之间共享状态时，才能将一个大型程序分解为更小的单元。这引出我们的下一个关注特质。

• 对可变状态的谨慎处理： 函数式编程有时候 (被半开玩笑地) 称为“面向值编程”。面向对象编程专注于类和对象的设计，每个类和对象都有它们自己的封装状态。然而，函数式编程强调基于值编程的重要性，这能使我们免受可变状态或其他一些副作用的困扰。通过避免可变状态，函数式程序比其对应的命令式或者面向对象的程序更容易组合。

• 类型： 最后，一个设计良好的函数式程序在使用类型时应该相当谨慎。精心选择你的数据和函数的类型，将会有助于构建你的代码，这比其他东西都重要。Swift 有一个强大的类型系统，使用得当的话，它能够让你的代码更加安全和健壮。

我们认为这些特质是 Swift 程序员可能从函数式编程社区学习到的精华点。在这本书中，我们将通过许多实例和学习案例说明以上几点。

根据我们的经验，学习用函数式的方式思考并不容易。它挑战了我们既有的熟练解决问题的方式。对于习惯写 for 循环的程序员来说，递归可能让我们倍感迷惑；赋值语句和全局状态的缺失让我们寸步难行；更不用提闭包，泛型，高阶函数和单子 (Monad)，这些东西简直让人痛不欲生。

在这本书中，我们假定你以前有过 Objective-C (或其他一些面向对象的语言) 的编程经验。书中不会涵盖 Swift 的基础知识，或是教你创建你的第一个 Xcode 工程，但我们会尝试在适当的时候引用现有的 Apple 文档。你应当能自如地阅读 Swift 程序，并且熟悉常见的编程概念，如类，方法和变量等。如果你刚刚开始学习编程，这本书可能并不适合你。

在这本书中，我们希望让函数式编程易于理解，并消除人们对它的一些偏见。使用这些理念去改善你的代码并不需要你拥有数学的博士学位！函数式编程并不是 Swift 编程的唯一方式。但是我们相信学习函数式编程会为你的工具箱添加一件重要的新工具，不论你使用那种语言，这件工具都会让你成为一个更好的开发者。

书籍更新

随着 Swift 的发展，我们会继续更新和改进这本书。如果你遇到任何错误，或者是想给我们其它类型的反馈，请在我们的 GitHub 仓库中创建一个 issue。

致谢

我们想要感谢众多帮助我们塑造了这本书的人。在此我们想要特别提及其中几位：

Natalye Childress 是我们的出版编辑。她给了我们很多宝贵的反馈意见，不仅保证了语言的正确性和一致性，而且确保了本书清晰易懂。

Sarah Lincoln 设计了本书的封面和布局。

Wouter 想要感谢乌得勒支大学允许他能够在这本书上投入时间进行编写。

我们还想要感谢测试版的读者们在本书写作过程中给予我们反馈(按字母顺序排列)：

Adrian Kosmaczewski, Alexander Altman, Andrew Halls, Bang Jun-young, Daniel Eggert, Daniel Steinberg, David Hart, David Owens II, Eugene Dorfman, f-dz-v, Henry Stamerjohann, J Bucaran, Jamie Forrest, Jaromir Siska, Jason Larsen, Jesse Armand, John Gallagher, Kaan Dedeoglu, Kare Morstol, Kiel Gillard, Kristopher Johnson, Matteo Piombo, Nicholas Outram, Ole Begemann, Rob Napier, Ronald Mannak, Sam Isaacson, Ssu Jen Lu, Stephen Horne, TJ, Terry Lewis, Tim Brooks, Vadim Shpakovski.

Chris, Florian, and Wouter

译序

随着程序语言的发展，我们作为软件开发人员，所熟知和使用的工具也在不断进化。以 Java 和 C++ 为代表的面向对象编程的编程方式在上世纪企业级的软件开发中大放异彩，然而随着软件行业不断发展，开发者们发现了面向对象范式的诸多不足。面向对象强调的是将与某数据类型相关的一系列操作都封装到该数据类型中去，因此，在数据类型中难免存在大量状态，以及相关的行为。虽然这很符合人类的逻辑直觉，但是当类型关系变得错综复杂的时候，类型中状态的改变和类型之间彼此的继承和依赖将使程序的复杂度几何上升。

避免使用程序状态和可变对象，是降低程序复杂度的有效方式之一，而这也正是函数式编程的精髓。函数式编程强调执行的结果，而非执行的过程。我们先构建一系列简单却具有一定功能的小函数，然后再将这些函数进行组装以实现完整的逻辑和复杂的运算，这是函数式编程的基本思想。

正如上面引言所述，Swift 是一门有着合适的语言特性来适配函数式编程方法的优秀语言。这个世界上最纯粹的函数式编程语言非 Haskell 莫属，但是由于我国程序开发的起步和热门相对西方世界要晚一些，使用 Haskell 的开发者可谓寥寥无几，因此 Haskell 在国内的影响力也十分有限。对于国内的不少开发者，特别是 iOS / OS X 的开发者来说，Swift 可能是我们第一次真正有机会去接触和使用的一门函数式特性语言。相比于很多已有的函数式编程语言，Swift 在语法上更加优雅灵活，语言本身也遵循了函数式的设计模式。作为函数式编程的入门语言，可以说 Swift 是非常理想的选择。而本书正是一本引领你进入 Swift 函数式编程世界的优秀读物，让更多的中国开发者有机会接触并了解 Swift 语言函数式的一面，正是我们翻译本书的目的所在。

本书大致上可以分为两个部分。首先，在第二章至第十章中，我们会介绍 Swift 函数式编程特性的一些基本概念，包括高阶函数的使用方法，不可变量的必要性，可选值的存在价值，枚举在函数式编程中的意义，以及纯函数式数据结构的优势等内容。这些都是函数式编程中的基本概念，也构成了 Swift 函数式特性甚至是这门语言的基础。当然，在这些概念讲解中我们也穿插了不少研究案例，以帮助读者真正理解这些基本概念，并对在何时使用它们以及使用它们为程序设计带来的改善形成直观印象。第二部分从第十一章开始，相比于前面的章节，这部分属于本书的进阶内容。我们将从构建最基本的生成器和序列开始，利用解析器组合算子构建一个解析器库，并最终实现一个相对复杂的公式解析器和函数式的表格应用。这部分内容环环相扣，因为内容抽象度较高，所以理解起来也可能比较困难。如果你在阅读最后表格应用章节时遇到麻烦的话，我们强烈建议你下载对应的完整源码进行研究，并且折回头去再次阅读第二部分的相关章节。随着你对各个函数式算子的深入理解，函数式编程的概念和思想将自然而然进入你的血液，这将丰富你的知识体系，并会对之后的开发工作大有裨益。

本书原版的三位作者都是富有经验的函数式编程方法的使用者或教师，他们将自己对于函数式编程的理解和 Swift 中的相关特性进行了对应和总结，并将这些联系揭示了出来。而中文版的三位译者花费了大量时间和精力，试图将这些规律以更易于理解的组织方式和语言，带给国内的开发者们。不过不论是原作者还是译者，其实和各位读者一样，都只不过是普通开发者中的一员，所以本书出现谬漏可能在所难免。如果您在阅读时发现了问题，可以给我们发邮件，或是在本书 issue 页面提出，我们将及时研究并加以改进。

事不宜迟，现在就让我们开始在函数式的世界中遨游一番吧。

陈聿菡，杜欣，王巍

函数式思想

函数在 Swift 中是一等值 (first-class-values)，换句话说，函数可以作为参数被传递到其它函数，也可以作为其它函数的返回值。如果你习惯了使用像是整型，布尔型或是结构体这样的简单类型来编程，那么这个理念可能看来非常奇怪。在本章中，我们会尽可能解释为什么一等函数是很有用的语言特性，并实际地提供本书的第一个函数式编程案例。

函数和方法将会贯穿整个章节。方法是函数的一种特殊情况：它是定义在类型里的函数。

案例：Battleship

我们将会用一个小案例来引出一等函数：这个例子是你在编写战舰类游戏时可能需要实现的一个核心函数。我们把将要看到的问题归结为，判断一个给定的点是否在射程范围内，并且距离友方船舶和我们自身都不太近。

首先，你可能会写一个很简单的函数来检验一个点是否在范围内。为了简明易懂，我们假定我们的船位于原点。这样一来，我们就可以将想要描述的区域形象化，如图 1：

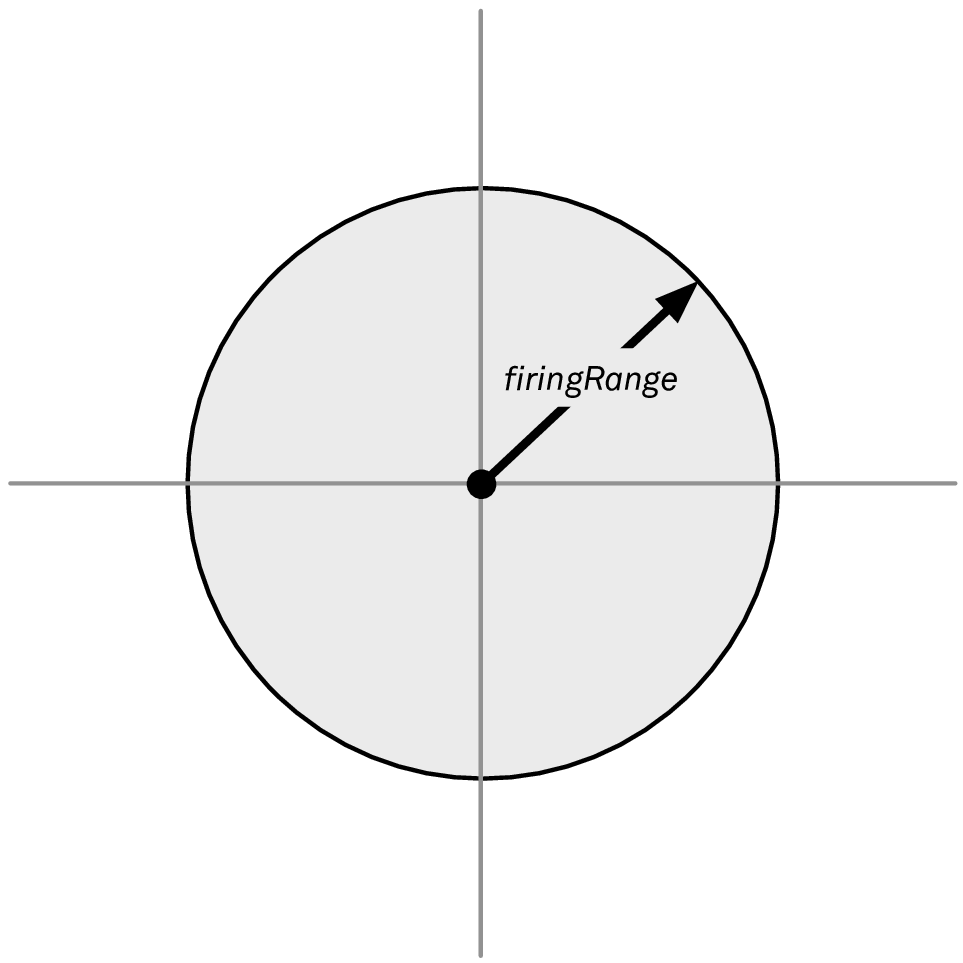
图 1: 位于原点的船舶射程范围内的点

首先，我们定义两种类型，Distance 和 Position：

typealias Distance = Double
    
    struct Position {
        var x: Double
        var y: Double
    }
    

注意，我们使用了 Swift 的 typealias 关键字，它允许我们为已经存在的类型创建一个别名。这里我们将 Distance 定义为 Double 的别名，目的在于让 API 的语义更清晰。

然后我们在 Position 中添加一个方法 within(range:)，用于检验一个点是否在图 1 中的灰色区域里。使用一些基础的几何知识，我们可以像下面这样定义这个函数：

extension Position {
        func within(range: Distance) -> Bool {
            return sqrt(x * x + y * y) <= range
        }
    }
    

如果假设我们总是位于原点，那现在这样就可以正常工作了。但是船舶还可能在原点以外的其它位置出现，我们可以更新一下形象化图，如图 2 所示：

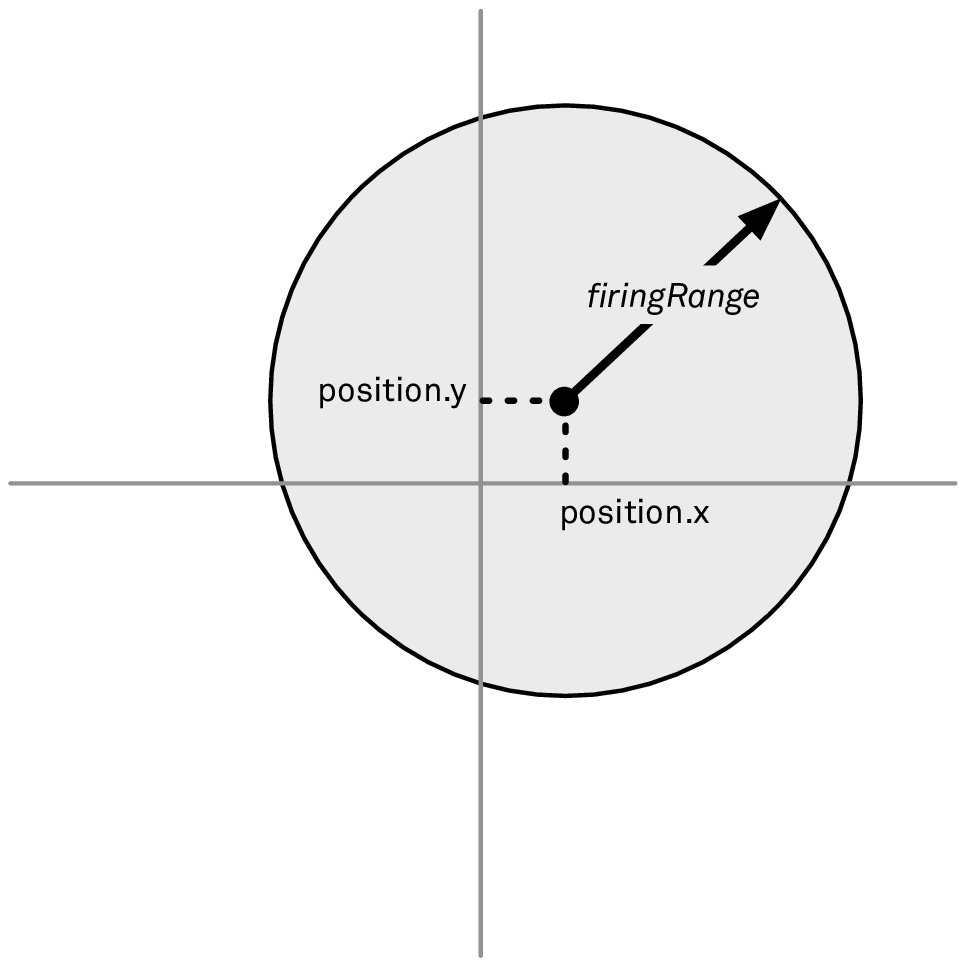
图 2: 允许船有它自己的位置

考虑到这一点，我们引入一个结构体 Ship，它有一个属性为 position：

struct Ship {
        var position: Position
        var firingRange: Distance
        var unsafeRange: Distance
    }
    

目前，姑且先忽略附加属性 unsafeRange。一会儿我们会回到这个问题。

我们向结构体 Ship 中添加一个 canEngage(ship:) 方法对其进行扩展，这个函数允许我们检验是否有另一艘船在范围内，不论我们是位于原点还是其它任何位置：

extension Ship {
        func canEngage(ship target: Ship) -> Bool {
            let dx = target.position.x - position.x
            let dy = target.position.y - position.y
            let targetDistance = sqrt(dx * dx + dy * dy)
            return targetDistance <= firingRange
        }
    }
    

也许现在你已经意识到，我们同时还想避免目标船舶离得过近。可以用图 3 来说明新情况，我们想要瞄准的仅仅只有那些对我们当前位置而言在 unsafeRange (不安全范围)外的敌人：

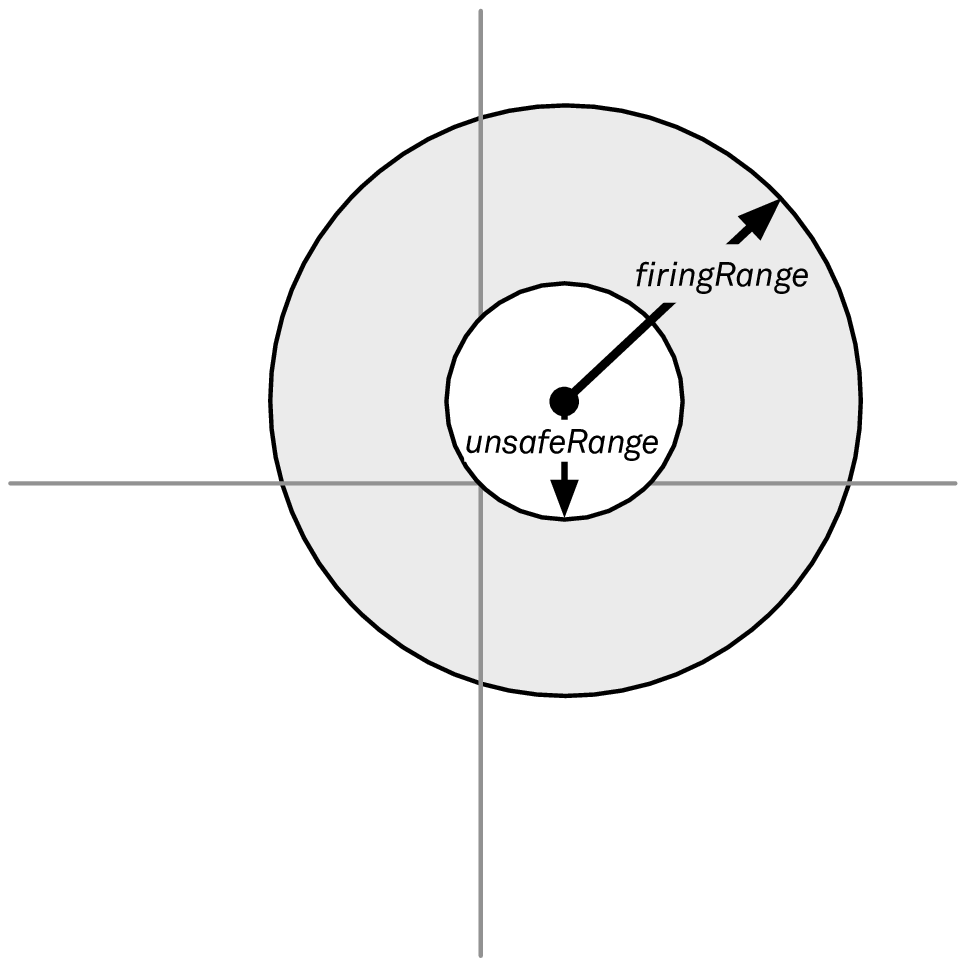
图 3: 避免与过近的敌方船舶交战

这样一来，我们需要再一次修改代码，使 unsafeRange 属性能够发挥作用：

extension Ship {
        func canSafelyEngage(ship target: Ship) -> Bool {
            let dx = target.position.x - position.x
            let dy = target.position.y - position.y
            let targetDistance = sqrt(dx * dx + dy * dy)
            return targetDistance <= firingRange && targetDistance > unsafeRange
        }
    } 
    

最后，我们还需要避免目标船舶过于靠近我方的任意一艘船。我们再一次将其形象化，见图 4：

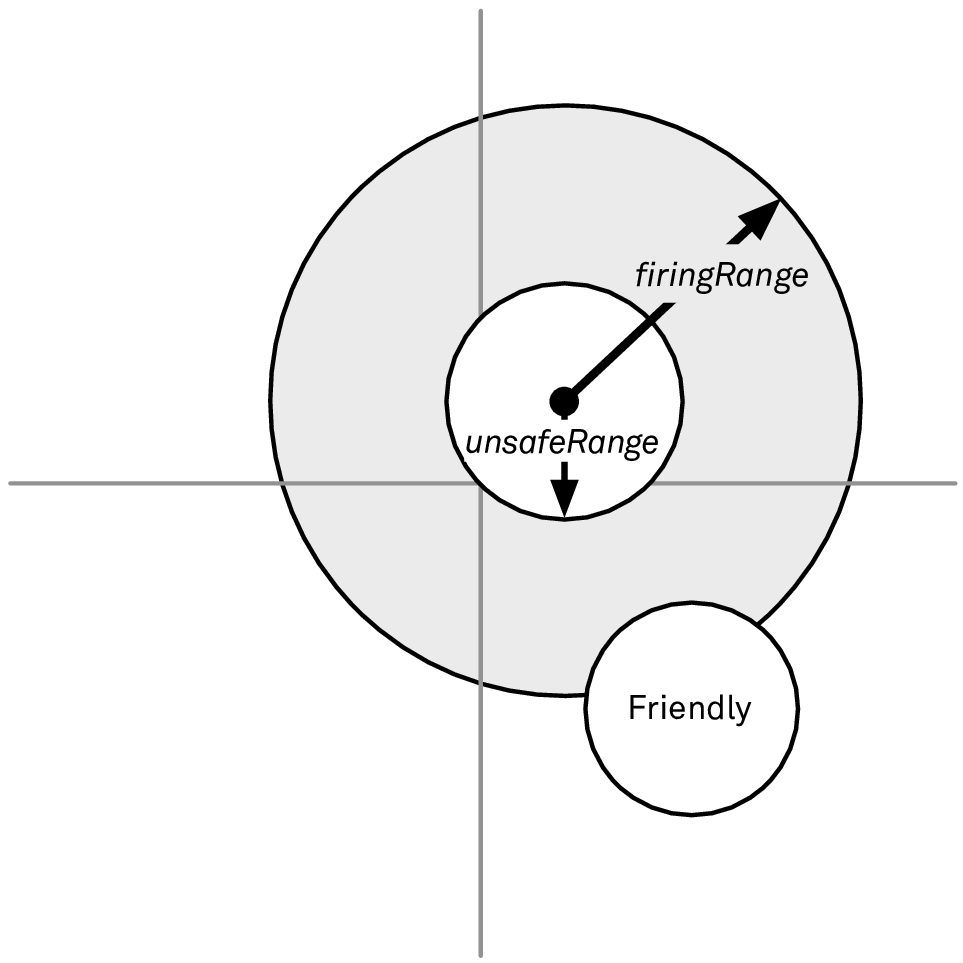
图 4: 避免敌方过于接近友方船舶

相应地，我们可以向 canSafelyEngage(ship:) 方法添加另一个参数代表友好船舶位置：

extension Ship {
        func canSafelyEngage(ship target: Ship, friendly: Ship) -> Bool {
            let dx = target.position.x - position.x
            let dy = target.position.y - position.y
            let targetDistance = sqrt(dx * dx + dy * dy)
            let friendlyDx = friendly.position.x - target.position.x
            let friendlyDy = friendly.position.y - target.position.y
            let friendlyDistance = sqrt(friendlyDx * friendlyDx +
                friendlyDy * friendlyDy)
            return targetDistance <= firingRange
                && targetDistance > unsafeRange
                && (friendlyDistance > unsafeRange)
        }
    }
    

随着代码逐渐发展，它变得越来越难以维护。这个方法包含了一大段复杂的运算代码，不过也没有那么糟，我们可以在 Position 中添加一个辅助方法和一个计算属性来负责几何运算，从而让这段代码变得清晰易懂一些：

extension Position {
        func minus(_ p: Position) -> Position {
            return Position(x: x - p.x, y: y - p.y)
        }
        var length: Double {
            return sqrt(x * x + y * y)
        }
    }
    

添加了辅助方法和属性之后，上述方法变成了下面这样：

extension Ship {
        func canSafelyEngage2(ship target: Ship, friendly: Ship) -> Bool {
            let targetDistance = target.position.minus(position).length
            let friendlyDistance = friendly.position.minus(target.position).length
            return targetDistance <= firingRange
                && targetDistance > unsafeRange
                && (friendlyDistance > unsafeRange)
        }
    }
    

现在的代码相较之前已经易读多了，但是我们还想更进一步，用一种声明式的方法来明确现有的问题。

一等函数

在当前 canSafelyEngage(ship:friendly) 的方法中，主要的行为是为构成返回值的布尔条件组合进行编码。在这个简单的例子中，虽然想知道这个函数做了什么并不是太难，但我们还是想要一个更模块化的解决方案。

我们已经在 Position 中引入了辅助方法使几何运算的代码更清晰易懂。用同样的方式，我们现在要添加一个函数，以更加声明式的方式来判断一个区域内是否包含某个点。

原来的问题归根结底是要定义一个函数来判断一个点是否在范围内。这样一个函数的类型应该是像下面这样的：

func pointInRange(point: Position) -> Bool {
        // 方法的具体实现
    }

由于该函数的类型将会非常重要，所以我们打算给它一个独立的名字：

typealias Region = (Position) -> Bool
    

从现在开始，Region 类型将指代把 Position 转化为 Bool 的函数。严格来说这不是必须的，但是它可以让我们更容易理解在接下来即将看到的一些类型。

我们使用一个能判断给定点是否在区域内的函数来代表一个区域，而不是定义一个对象或结构体来表示它。如果你不习惯函数式编程，这可能看起来会很奇怪，但是记住：在 Swift 中函数是一等值！我们有意识地选择了 Region 作为这个类型的名字，而非 CheckInRegion 或 RegionBlock 这种字里行间暗示着它们代表一种函数类型的名字。函数式编程的核心理念就是函数是值，它和结构体、整型或是布尔型没有什么区别 —— 对函数使用另外一套命名规则会违背这一理念。

我们现在要写几个函数来创建、控制和合并各个区域。

我们定义的第一个区域是以原点为圆心的圆 (circle)：

func circle(radius: Distance) -> Region {
        return { point in point.length <= radius }
    }
    

值得注意的是，以半径 r 为参数，调用 circle(radius: r) 返回的是一个函数。这里我们使用了 Swift 的闭包来构造我们期待的返回函数。给定一个表示位置的参数 point，然后检查该 point 是否在以原点为中心且给定半径的圆所限定的区域中。

当然，并不是所有圆的圆心都是原点。我们可以给 circle 函数添加更多的参数来解决这个问题。要得到一个圆心是任意定点的圆，我们只需要添加另一个代表圆心的参数，并确保在计算新区域时将这个参数考虑进去：

func circle2(radius: Distance, center: Position) -> Region {
        return { point in point.minus(center).length <= radius }
    }
    

然而，如果我们想对更多的图形组件 (例如，想象我们不仅有圆，还有矩形或其它形状) 做出同样的改变，可能需要重复这些代码。更加函数式的方式是写一个区域变换函数。这个函数按一定的偏移量移动一个区域：

func shift(_ region: @escaping Region, by offset: Position) -> Region {
        return { point in region(point.minus(offset)) }
    }
    

当需要在函数返回之后使用其参数（如：region）时，该参数需要被标记为 @escaping。即使忘记标记，编译器也将会提醒我们。如果你想了解更详细的信息，请参阅 Apple 的 The Swift Programming Language 一书中《逃逸闭包》的部分。

调用 shift(region, by: offset) 函数会将区域向右上方移动，偏移量分别是 offset.x 和 offset.y。我们需要的是一个传入 Position 并返回 Bool 的函数 Region。为此，我们需要另写一个闭包，它接受我们要检验的点，这个点减去偏移量之后我们得到一个新的点。最后，为了检验新点是否在原来的区域内，我们将它作为参数传递给 region 函数。

这是函数式编程的核心概念之一：为了避免创建像 circle2 这样越来越复杂的函数，我们编写了一个 shift(_:by:) 函数来改变另一个函数。例如，一个圆心为 (5, 5) 半径为 10 的圆，可以用下面的方式表示：

let shifted = shift(circle(radius: 10), by: Position(x: 5, y: 5))
    

还有很多其它的方法可以变换已经存在的区域。例如，也许我们想要通过反转一个区域以定义另一个区域。这个新产生的区域由原区域以外的所有点组成：

func invert(_ region: @escaping Region) -> Region {
        return { point in !region(point) }
    }
    

我们也可以写一个函数将既存区域合并为更大更复杂的区域。比如，下面两个函数分别可以计算参数中两个区域的交集和并集：

func intersect(_ region: @escaping Region, with other: @escaping Region)
        -> Region {
        return { point in region(point) && other(point) }
    }
    
    func union(_ region: @escaping Region, with other: @escaping Region)
        -> Region {
        return { point in region(point) || other(point) }
    }
    

当然，我们可以利用这些函数来定义更丰富的区域。difference 函数接受两个区域作为参数 —— 原来的区域和要减去的区域 —— 然后为所有在第一个区域中且不在第二个区域中的点构建一个新的区域：

func subtract(_ region: @escaping Region, from original: @escaping Region)
        -> Region {
        return intersect(original, with: invert(region))
    }
    

这个例子告诉我们，在 Swift 中计算和传递函数的方式与整型或布尔型没有任何不同。这让我们能够写出一些基础的图形组件 (比如圆)，进而能以这些组件为基础，来构建一系列函数。每个函数都能修改或是合并区域，并以此创建新的区域。比起写复杂的函数来解决某个具体的问题，现在我们完全可以通过将一些小型函数装配起来，广泛地解决各种各样的问题。

现在让我们把注意力转回原来的例子。关于区域的小型函数库已经准备就绪，我们可以像下面这样重构 canSafelyEngage(ship:friendly:) 这个复杂的方法：

extension Ship {
        func canSafelyEngage(ship target: Ship, friendly: Ship) -> Bool {
            let rangeRegion = subtract(circle(radius: unsafeRange),
                from: circle(radius: firingRange))
            let firingRegion = shift(rangeRegion, by: position)
            let friendlyRegion = shift(circle(radius: unsafeRange),
                by: friendly.position)
            let resultRegion = subtract(friendlyRegion, from: firingRegion)
            return resultRegion(target.position)
        }
    }
    

这段代码定义了两个区域：firingRegion 和 friendlyRegion。通过计算这两个区域的差集 (即在 firingRegion 中且不在 friendlyRegion 中的点的集合)，我们可以得到我们感兴趣的区域。将这个区域函数作用在目标船舶的位置上，我们就可以计算所需的布尔值了。

面对同一个问题，与原来的 canSafelyEngage(ship:friendly:) 方法相比，使用 Region 方法重构后的版本是更加声明式的解决方案。我们坚信后一个版本会更容易理解，因为我们的解决方案是装配式的。你可以探究组成它的每个部分，例如 firingRegion 和 friendlyRegion，看一看它们是如何被装配并解决原来的问题的。另一方面，原来庞大的方法混合了各个组成区域的描述语句和描述它们所需要的算式。通过定义我们之前提出的辅助函数将这些关注点进行分离，显著提高了复杂区域的组合性和易读性。

能做到这样，一等函数是至关重要的。虽然 Objective-C 也支持一等函数，或者说是 block，即使可以做到类似的事情，但难掩遗憾，在 Objective-C 中使用 block 十分繁琐。一部分原因是因为语法问题：block 的声明和 block 的类型与 Swift 的对应部分相比并不是那么简单。在后面的章节中，我们也将看到泛型如何让一等函数更加强大，远比 Objective-C 中用 blocks 实现更加容易。

我们定义 Region 类型的方法有它自身的缺点。我们选择了将 Region 类型定义为简单类型，并作为 (Position) -> Bool 函数的别名。其实，我们也可以选择将其定义为一个包含单一函数的结构体：

struct Region {
        let lookup: (Position) -> Bool
    }
    

接下来我们可以用 extensions 的方式为结构体定义一些类似的方法，来代替对原来的 Region 类型进行操作的自由函数。这可以让我们能够通过对区域进行反复的函数调用来变换这个区域，直至得到需要的复杂区域，而不用像以前那样将区域作为参数传递给其他函数：

rangeRegion.shift(ownPosition).difference(friendlyRegion)
    

这种方法有一个优点，它需要的括号更少。再者，这种方式下 Xcode 的自动补全在装配复杂的区域时会十分有用。不过，为了便于展示，我们选择了使用简单的 typealias 以突出在 Swift 中使用高阶函数的方法。

此外，值得指出的是，现在我们不能够看到一个区域是如何被构建的：它是由更小的区域组成的吗？还是单纯只是一个以原点为圆心的圆？我们唯一能做的是检验一个给定的点是否在区域内。如果想要形象化一个区域，我们只能对足够多的点进行采样来生成 (黑白) 位图。

在后面的章节中，我们将使用另外一种设计，来帮助你解答这些问题。

我们在本章节，或者说是整本书中使用的命名方式稍有违背 Swift API 设计指南。Swift 指南要求在设计时考虑方法名。例如，如果 intersect 被定义为一个方法，那么该方法名应该为 intersecting 或 intersected，因为返回值是一个新值，而非对现有区域进行修改。尽管如此，在编写顶级函数时，我们决定使用 intersect 这样的基本形式。

类型驱动开发

在引言中，我们提到了函数式编程可以用规范的方式将函数作为参数装配为规模更大的程序。在本章中，我们看到了一个以这种函数式方式设计的具体例子。我们定义了一系列函数来描述区域。每一个函数单打独斗的话都并不强大。然而装配到一起时，却可以描述你绝不会想要从零开始编写的复杂区域。

解决的办法简单而优雅。这与单纯地将 canSafelyEngage(ship:friendly:) 方法拆分为几个独立的方法那种重构方式是完全不同的。我们确定了如何来定义区域，这是至关重要的设计决策。当我们选择了 Region 类型之后，其它所有的定义就都自然而然，水到渠成了。这个例子给我们的启示是，我们应该谨慎地选择类型。这比其他任何事都重要，因为类型将左右开发流程。

注解

本章提供的代码受到了一个 Haskell 解决方案的启发，该方案解决了由美国高等研究计划局 (ARPA) 的 Hudak and Jones (1994) 提出的一个问题。

Objective-C 通过引入 blocks 实现了对一等函数的支持：你可以将函数和闭包作为参数并轻松地使用内联的方式定义它们。然而，在 Objective-C 中使用它们并不像在 Swift 中一样方便，尽管两者在语意上完全相同。

从历史上看，一等函数的理念可以追溯到 Church 的 lambda 演算 (Church 1941; Barendregt 1984)。此后，包括 Haskell，OCaml，Standard ML，Scala 和 F# 在内的大量 (函数式) 编程语言都不同程度地借鉴了这个概念。

案例研究：封装 Core Image

前一章介绍了高阶函数的概念，并展示了将函数作为参数传递给其它函数的方法。不过，使用的例子可能与你日常写的“真实”代码相去甚远。在本章中，我们将会围绕一个已经存在且面向对象的 API，展示如何使用高阶函数将其以小巧且函数式的方式进行封装。

Core Image 是一个强大的图像处理框架，但是它的 API 有时可能略显笨拙。Core Image 的 API 是弱类型的 —— 我们通过键值编码 (KVC) 来配置图像滤镜 (filter)。在使用参数的类型或名字时，我们都使用字符串来进行表示，这十分容易出错，极有可能导致运行时错误。而我们开发的新 API 将会利用类型来避免这些原因导致的运行时错误，最终我们将得到一组类型安全而且高度模块化的 API。

即使你不熟悉 Core Image，或者不能完全理解本章代码片段的细节，也大可不必担心。我们的目标并不是围绕 Core Image 构建一个完整的封装，而是要说明如何把像高阶函数这样的函数式编程概念运用到实际的生产代码中。

滤镜类型

CIFilter 是 Core Image 中的核心类之一，用于创建图像滤镜。当实例化一个 CIFilter 对象时，你 (几乎) 总是通过 kCIInputImageKey 键提供输入图像，再通过 outputImage 属性取回处理后的图像。取回的结果可以作为下一个滤镜的输入值。

在本章即将开发的 API 中，我们会尝试封装应用这些键值对的具体细节，从而呈现给用户一个安全的强类型 API。我们将 Filter 类型定义为一个函数，该函数接受一个图像作为参数并返回一个新的图像：

typealias Filter = (CIImage) -> CIImage
    

我们将以这个类型为基础进行后续的构建。

构建滤镜

现在我们已经定义了 Filter 类型，接着就可以开始定义函数来构建特定的的滤镜了。这些函数在接受特定滤镜所需要的参数之后，构造并返回一个 Filter 类型的值。它们的基本形态大概都是下面这样：

func myFilter(...) -> Filter
    

注意这里的返回值 Filter，也是一个函数。稍后我们将会借助它来组合多个滤镜以实现期待的图像效果。

模糊

让我们来定义第一个简单的滤镜 —— 高斯模糊滤镜。定义它只需要模糊半径这一个参数：

func blur(radius: Double) -> Filter {
        return { image in
            let parameters: [String: Any] = [
                kCIInputRadiusKey: radius,
                kCIInputImageKey: image
            ]
            guard let filter = CIFilter(name: "CIGaussianBlur",
                withInputParameters: parameters) 
                else { fatalError() }
            guard let outputImage = filter.outputImage 
                else { fatalError() }
            return outputImage
        }
    }
    

一切就是这么简单。blur 函数返回一个新函数，新函数接受一个 CIImage 类型的参数 image，并返回一个新图像 (return filter.outputImage)。因此，blur 函数的返回值满足我们之前定义的 (CIImage) -> CIImage，也就是 Filter 类型。

CIFilter 的初始化及 filter 的 outputImage 属性都返回可选值，我们使用了 guard 语句来解包这些可选值。如果这些值中有 nil，那么就意味着发生了程序错误的情况。比方说，如果我们向滤镜传递了错误的参数，就会导致这种情况。结合 fatalError() 使用 guard 语句而非强制解包可选值使得这种意图更明显。

这个例子仅仅只是对 Core Image 中一个已经存在的滤镜进行的简单封装。我们可以反复使用相同的模式来创建自己的滤镜函数。

颜色叠层

现在让我们来定义一个能够在图像上覆盖纯色叠层的滤镜。Core Image 默认不包含这样一个滤镜，但是我们完全可以用已经存在的滤镜来组成它。

我们将使用的两个基础组件：颜色生成滤镜 (CIConstantColorGenerator) 和图像覆盖合成滤镜 (CISourceOverCompositing)。首先让我们来定义一个生成固定颜色的滤镜：

func generate(color: UIColor) -> Filter {
        return { _ in
            let parameters = [kCIInputColorKey: CIColor(cgColor: color.cgColor)]
            guard let filter = CIFilter(name: "CIConstantColorGenerator",
                withInputParameters: parameters) 
                else { fatalError() }
            guard let outputImage = filter.outputImage 
                else { fatalError() }
            return outputImage
        }
    }
    

这段代码看起来和我们用来定义模糊滤镜的代码非常相似，但是有一个显著的区别：颜色生成滤镜不检查输入图像。因此，我们不需要给返回函数中的图像参数命名。取而代之，我们使用一个匿名参数 _ 来强调滤镜的输入图像参数是被忽略的。

接下来，我们将要定义合成滤镜：

func compositeSourceOver(overlay: CIImage) -> Filter {
        return { image in
            let parameters = [
                kCIInputBackgroundImageKey: image,
                kCIInputImageKey: overlay
            ]
            guard let filter = CIFilter(name: "CISourceOverCompositing",
                withInputParameters: parameters) 
                else { fatalError() }
            guard let outputImage = filter.outputImage 
                else { fatalError() }
            return outputImage.cropping(to: image.extent)
        }
    }
    

在这里我们将输出图像剪裁为与输入图像一致的尺寸。严格来说，这不是必须的，完全取决于我们希望滤镜如何工作。不过，这个选择在我们即将涉及的例子中效果很好。

最后，我们通过结合两个滤镜来创建颜色叠层滤镜：

func overlay(color: UIColor) -> Filter {
        return { image in
            let overlay = generate(color: color)(image).cropping(to: image.extent)
            return compositeSourceOver(overlay: overlay)(image)
        }
    }
    

我们再次返回了一个接受图像作为参数的函数。我们在定义该函数的整个过程中所做的一切可大致概括为：首先使用先前定义的颜色生成滤镜函数 generate(color:) 来生成一个新叠层。然后以颜色作为参数调用该函数，返回 Filter 类型值。而 Filter 类型本身就是一个从 CIImage 到 CIImage 的函数，因此我们还可以向 generate(color:) 函数传递一个 image 参数，最终通过计算能够得到一个 CIImage 类型的新叠层。

与叠层的创建相似，所构建的滤镜函数的返回值也有着相同的结构：先通过调用 compositeSourceOver(overlay:) 来创建一个滤镜。然后以输入图像为参数调用这个滤镜。

组合滤镜

到现在为止，我们已经定义了模糊滤镜和颜色叠层滤镜，可以把它们组合在一起使用：首先将图像模糊，然后再覆盖上一层红色叠层。让我们来载入一张图片试试看：

let url = URL(string: "http://www.objc.io/images/covers/16.jpg")!
    let image = CIImage(contentsOf: url)!
    

现在我们可以链式地将两个滤镜应用到载入的图像上：

let radius = 5.0
    let color = UIColor.red.withAlphaComponent(0.2)
    let blurredImage = blur(radius: radius)(image)
    let overlaidImage = overlay(color: color)(blurredImage)
    

我们再一次通过创建滤镜来处理图像，例如先创建 blur(radius:radius) 滤镜，随后将其运用到图像上。

复合函数

当然，我们可以将上面代码里两个调用滤镜的表达式简单合为一体：

let result = overlay(color: color)(blur(radius: radius)(image))
    

然而，由于括号错综复杂，这些代码很快失去了可读性。更好的解决方式是构建一个可以将滤镜合二为一的函数：

func compose(filter filter1: @escaping Filter, 
        with filter2: @escaping Filter) -> Filter 
    {
        return { image in filter2(filter1(image)) }
    }
    

compose(filter:with:) 函数接受两个 Filter 类型的参数，并返回一个新滤镜。这个复合滤镜接受一个 CIImage 类型的图像参数，然后将该参数传递给 filter1，取得返回值之后再传递给 filter2。这里我们举一个例子，来阐述我们可以如何使用 compose(filter:with:) 定义自己的复合滤镜：

let blurAndOverlay = compose(filter: blur(radius: radius), 
        with: overlay(color: color))
    let result1 = blurAndOverlay(image)
    

为了让代码更具可读性，我们还可以再进一步，为组合滤镜引入自定义运算符。诚然，随意自定义运算符并不一定对提升代码可读性有帮助。不过，在图像处理库中，滤镜的组合是一个反复被讨论的问题。一旦你知道了这个运算符，滤镜的定义也会随之变得易读：

infix operator >>>
    
    func >>>(filter1: @escaping Filter, filter2: @escaping Filter) -> Filter {
        return { image in filter2(filter1(image)) }
    }
    

现在我们可以使用 >>> 运算符达到与之前使用 compose(filter:with:) 相同的目的：

let blurAndOverlay2 = 
        blur(radius: radius) >>> overlay(color: color)
    let result2 = blurAndOverlay2(image)
    

由于运算符 >>> 默认是左结合的 (left-associative)，就像 Unix 的管道一样，因此滤镜将以从左到右的顺序被应用到图像上。

我们定义的组合滤镜运算符是一个复合函数的例子。在数学中，f 和 g 两个函数构成的复合函数有时候被写作 f · g，表示定义的新函数将输入的 x 映射到 f(g(x))。除了顺序，这恰恰也是我们的 >>> 运算符所做的：将一个图像参数传递给运算符操作的两个滤镜。

理论背景：柯里化

在本章中，我们已经反复写了好多次类似下面这样的代码：

blur(radius: radius)(image)
    

先调用一个函数，该函数返回新函数 (本例指 Filter)，然后传入另一个参数并调用之前返回的新函数。事实上也可以简单地传递两个参数给 blur 函数，然后直接返回图像，两者效果完全相同：

let blurredImage = blur(image: image, radius: radius)
    

写一个函数返回另一个函数，只是为了再次调用被返回的函数。为什么我们要选择这个看似更复杂的方式呢？

结合上文我们知道，有两种等效的方式能够定义一个可以接受两个 (或更多) 参数的函数。对于大多数程序员来说，应该会觉得第一种风格更熟悉：

func add1(_ x: Int, _ y: Int) -> Int {
        return x + y
    }
    

add1 函数接受两个整型参数并返回它们的和。然而在 Swift 中，我们对该函数的定义还可以有另一个版本：

func add2(_ x: Int) -> ((Int) -> Int) {
        return { y in x + y }
    }
    

这里的 add2 函数接受第一个参数 x 之后，返回一个闭包，然后再接受第二个参数 y。这与滤镜函数的结构一模一样。

因为该函数的箭头向右结合 (right-associative)，所以我们可以移除包围在结果函数类型周围的括号。从而得到本质上与 add2 完全等价的函数 add3：

func add3(_ x: Int) -> (Int) -> Int {
        return { y in x + y }
    }
    

add1 与 add2 的区别在于调用方式：

add1(1, 2) // 3
    add2(1)(2) // 3
    

在第一种方法中，我们将两个参数同时传递给 add1；而第二种方法则首先向函数传递第一个参数 1，然后将返回的函数应用到第二个参数 2。两个版本是完全等价的：我们可以根据 add2 来定义 add1，反之亦然。

add1 和 add2 的例子向我们展示了如何将一个接受多参数的函数变换为一系列只接受单个参数的函数，这个过程被称为柯里化 (Currying)，它得名于逻辑学家 Haskell Curry；我们将 add2 称为 add1 的柯里化版本。

那么，为什么说柯里化很有趣呢？正如迄今为止我们在本书中所看到的，在一些情况下，你可能想要将函数作为参数传递给其它函数。如果我们有像 add1 一样未柯里化的函数，那我们就必须同时用到它的全部两个参数来调用这个函数。然而，对于一个像 add2 一样被柯里化了的函数来说，我们有两个选择：可以使用一个或两个参数来调用。

在本章中为了创建滤镜而定义的函数全部都已经被柯里化了 —— 它们都接受一个附加的图像参数。按照柯里化风格来定义滤镜，我们可以很容易地使用 >>> 运算符将它们进行组合。假如我们用这些函数未柯里化的版本来构建滤镜的话，虽然依然可以写出相同的滤镜，但是这些滤镜的类型将根据它们所接受的参数不同而略有不同。这样一来，想要为这些不同类型的滤镜定义一个统一的组合运算符就要比现在困难得多了。

讨论

这个例子再一次阐释了将复杂的代码拆解为小块的方式，而这些小块可以使用函数的方式进行重新装配，并形成完整的功能。本章的目标并不是为 Core Image 定义一个完整的 API，而是想说明在更实际的案例中如何使用高阶函数和复合函数。

为什么要做这么多努力呢？事实上 Core Image API 已经很成熟并能够提供几乎所有你可能需要的功能。但是尽管如此，我们相信本章所设计的 API 也有一些优点：

• 安全 — 使用我们构筑的 API 几乎不可能发生由未定义键或强制类型转换失败导致的运行时错误。

• 模块化 — 使用 >>> 运算符很容易将滤镜进行组合。这样你可以将复杂的滤镜拆解为更小，更简单，且可复用的组件。此外，组合滤镜与组成它的组件是完全相同的类型，所以你可以交替使用它们。

• 清晰易懂 — 即使你从未使用过 Core Image，也应该能够通过我们定义的函数来装配简单的滤镜。你完全不需要关心 kCIInputImageKey 或 kCIInputRadiusKey 这样的特定键如何进行初始化。单看类型，你几乎就能够知道如何使用 API，甚至不需要更多文档。

我们的 API 提供了一系列能够用来定义和组合滤镜的函数。使用和复用任何自定义的滤镜都是安全的。每个滤镜都能被独立测试和理解。比起原来的 Core Image API，我们的设计会更让人偏爱。如果要说理由的话，相信上面几点足够让人信服。

Map、Filter 和 Reduce

接受其它函数作为参数的函数有时被称为高阶函数。在 Swift 标准库中就有几个作用于数组的高阶函数，本章中，我们将对它们进行探索。伴随这个过程，同时将介绍 Swift 的泛型，以及展示如何将复杂计算运用于数组。

泛型介绍

Filter

Reduce

实际运用

泛型和 Any 类型

注释

可选值

Swift 的可选类型可以用来表示可能缺失或是计算失败的值。本章将介绍如何有效地利用可选类型，以及它们在函数式编程范式中的使用方式。

案例研究：字典

玩转可选值

为什么使用可选值？

案例研究：QuickCheck

近些年来，在 Objective-C 中，测试变得越来越普遍。现在有许多流行的库通过持续集成工具来进行自动化测试。XCTest 是用来写单元测试的标准框架。此外，很多第三方框架 (例如 Specta、 Kiwi 和 FBSnapshotTestCase) 也已经可供使用，同时现阶段还有若干 Swift 的新框架正在开发中。

所有的这些框架都遵循一个相似的模式：测试通常由一些代码片段和预期结果组成。执行代码之后，将它的结果与测试中定义的预期结果相比较。不同的库测试的层次会有所不同 —— 有的测试独立的方法，有的测试类，还有一些执行集成测试 (运行整个应用)。在本章中，我们将通过迭代的方法，一步一步完善并最终构建一个针对 Swift 函数进行“特性测试 (property-based testing)”的小型库。

在写单元测试的时候，输入数据是程序员定义的静态数据。比方说，在对一个加法进行单元测试时，我们可能会写一个验证 1 + 1 等于 2 的测试。如果加法的实现方式破坏了这个特性，测试就会失败。不过，为了更一般化，我们可以选择测试加法的交换律 —— 换句话说，就是验证 a + b 等于 b + a。为了进行这项测试，我们可以写一个测试用例来验证 42 + 7 等于 7 + 42。

QuickCheck (Claessen and Hughes 2000) 是一个用于随机测试的 Haskell 库。相较于独立的单元测试中每个部分都依赖特定输入来测试函数是否正确，QuickCheck 允许你描述函数的抽象特性并生成测试来验证这些特性。当一个特性通过了测试，就没有必要再证明它的正确性。更确切地说，QuickCheck 旨在找到证明特性错误的临界条件。在本章中，我们将用 Swift (部分地) 移植 QuickCheck 库。

这里举例说明会比较好。假设我们想要验证加法是一个满足交换律的运算。于是，首先为两个整型数值 x 和 y 写了一个函数，来检验 x + y 与 y + x 是否相等：

func plusIsCommutative(x: Int, y: Int) -> Bool {
        return x + y == y + x
    }
    

用 QuickCheck 检验这条语句就像调用 check 函数一样简单：

check("Plus should be commutative", plusIsCommutative)
    
    /** 打印：
        "Plus should be commutative" passed 10 tests.
    */
    

构建 QuickCheck

缩小范围

展望

不可变性的价值

Swift 有一些机制，用于控制值的变化方式。在本章中，我们将介绍这些不同的机制是如何工作的，以及如何区别值类型和引用类型，并证明为什么限制可变状态的使用是一个良好的理念。

变量和引用

值类型与引用类型

讨论

枚举

在设计和实现 Swift 应用时，类型扮演着非常重要的角色，这也是本书想说明的重点之一。在这一章，我们将介绍 Swift 中的枚举类型。借此，你可以创建更为严密的类型，来表示应用中使用的数据。

关于枚举

关联值

添加泛型

Swift 中的错误处理

再聊聊可选值

数据类型中的代数学

为什么使用枚举？

纯函数式数据结构

在前面的章节中，我们了解了如何利用枚举针对正在开发的应用来定义特定类型。而本章中，我们会定义可递归的枚举，并向大家展示，如何利用这个特性来定义一些高性能且非可变的数据结构。

所谓纯函数式数据结构 (Purely Functional Data Structures) 指的是那些具有不变性的高效的数据结构。像 C 或 C++ 这样的指令式语言中的数据结构往往是可变的，直接将这类数据结构使用在函数式语言中往往会水土不服。通过本章，我们想向您展示函数式语言中的纯函数式数据结构的构建方式和特点。

二叉搜索树

基于字典树的自动补全

讨论

案例研究：图表

在本章中，我们会看到一种描述图表的函数式方式，并讨论如何利用 Core Graphics 来绘制它们。通过对 Core Graphic 进行一层函数式的封装，可以得到一个更简单且易于组合的 API。

绘制正方形和圆

核心数据结构

额外的组合算子

讨论

迭代器和序列

在本章中，我们将关注点放在了迭代器 (Iterators) 和序列 (Sequences) 上，正是它们，组成了 Swift 中 for 循环的基础体系。

迭代器

序列

案例研究：遍历二叉树

案例研究：优化 QuickCheck 的范围收缩

案例研究：解析器组合算子

在试图将一系列符号 (通常是一组字符) 转换为结构化的数据时，解析器 (parser) 是一个非常有用的工具。有些时候，你可以使用正则表达式作为替代，来解析一串简单的字符串，但正则表达式能做的事很有限，且难以在短时间内理解其含义。一旦你知道了如何去编写一个解析器 (或是如何使用一个已有的解析器库)，它就会变成你工具箱中非常有用的工具之一。

想要创建一个解析器，通常有这样几种方式：首先，你可以手工编码解析器，通过使用类似于标准库里 Scanner 类的这样的辅助工具，或许会让整个过程变得简单一些。或者，你可以使用额外的工具来生成一个解析器，比如 Bison 或是 YACC。又或是，你可以使用一个解析器组合算子库，在很多情况下，与之前各有优劣的两种方案相比，这种方案会更为折中。

解析器组合算子是一种函数式的解析方案。不同于对解析器的可变状态进行管理 (比如我们即将要处理的字符)，解析器组合算子使用纯函数来避免可变状态。在本章，我们将探索解析器组合算子的工作方式，同时自行编写一些解析器组合算子库的核心部件。作为本章的示例，我们将尝试解析类似 1+2*3 这样简单的算术表达式。

我们的目标并非编写一个全面的组合算子库，而只是学习解析器组合算子库背后的工作原理，以便你能够毫不费力地使用它们。相对于自己编写来说，在大部分情况下，使用一个已有的库总是更好的选择。

解析器的类型

组合解析器

解析算术表达式

更 Swift 化的解析器类型

案例研究：构建一个表格应用

在本章中，我们将对上一章中用于解析算术表达式的代码进行拓展，并基于这些代码构建出一个简易的电子表格应用。我们会把这项工作分为三步：首先，我们要为希望被解析的表达式编写解析器；然后，我们会为这些表达式编写一个求值器；最后，我们会将以上代码嵌入一套简单的用户界面中。

解析

求值

用户界面

函子、适用函子与单子

在本章中，我们会解释一些函数式编程中的专用术语和一些常见模式，比如函子 (Functor)、适用函子 (Applicative Functor) 和单子 (Monad) 等。理解这些常见的模式，会有助于你设计自己的数据类型，并为你的 API 选择更合适的函数。

函子

迄今为止，我们已经遇到了几个被命名为 map 的方法，类型分别如下：

extension Array {
        func map<R>(transform: (Element) -> R) -> [R]
    }
    extension Optional {
        func map<R>(transform: (Wrapped) -> R) -> R?
    }
    
    extension Parser {
        func map<T>(_ transform: @escaping (Result) -> T) -> Parser<T> 
    }
    

为什么这三个截然不同的方法会拥有相同的方法名呢？要回答这个问题，我们需要先探究这三个方法的相似之处。在开始之前，将 Swift 使用的一些简写符号进行展开会帮助我们更容易理解发生了什么。像 Int? 这样的可选值也可以被显式地写作 Optional<Int>。同样地，我们也可以使用 Array<T> 来替换 [T]。如果我们按照上面的书写方式定义数组和可选值的 map 方法，相似之处就变得明显了起来：

extension Array {
        func map<R>(transform: (Element) -> R) -> Array<R>
    }
    extension Optional {
        func map<R>(transform: (Wrapped) -> R) -> Optional<R>
    }
    
    extension Parser {
        func map<T>(_ transform: @escaping (Result) -> T) -> Parser<T> 
    }
    

Optional 与 Array 都是需要一个泛型作为参数来构建具体类型的类型构造体 (Type Constructor)。对于一个实例来说，Array<T> 与 Optional<Int> 是合法的类型，而 Array 本身却并不是。每个 map 方法都需要两个参数：一个即将被映射的数据结构，和一个类型为 (T) -> U 的函数 transform。对于数组或可选值参数中所有类型为 T 的值，map 方法会使用 transform 将它们转换为 U。这种支持 map 运算的类型构造体 —— 比如可选值或数组 —— 有时候也被称作函子 (Functor)。

实际上，我们之前定义的很多类型都是函子。比如，我们可以为第八章中的 Result 类型实现一个 map 方法：

extension Result {
        func map<U>(f: (T) -> U) -> Result<U> {
            switch self {
            case let .success(value): return .success(f(value))
            case let .error(error): return .error(error)
            }
        }
    }
    

类似地，我们之前看到的二叉搜索树、字典树以及解析器组合算子等类型都是函子。函子有时会被描述为一个储存特定类型值的“容器”。而 map 方法则用来对储存在容器中的值进行转换。作为一个直观的印象，这样理解或许会有帮助，但却有点过于狭隘。还记得我们在第二章中看到的 Region 类型么？

struct Position {
        var x: Double
        var y: Double
    }
    

typealias Region = (Position) -> Bool
    

如果只使用 Region 的定义 (一个返回布尔值的函数)，我们至多能生成一些非黑即白的位图。可以将这个定义泛型化，对每一个位置关联信息的类型做一次抽象：

struct Region<T> {
        let value: (Position) -> T
    }
    

通过这样的定义，我们可以为每个位置关联一个布尔值、RGB 色值、或者任意其他的信息。我们甚至还可以为这些泛型区域定义一个 map 方法。实际上，上述定义可以被归纳为一个复合函数：

extension Region {
        func map<U>(transform: @escaping (T) -> U) -> Region<U> {
            return Region<U> { pos in transform(self.value(pos)) }
        }
    }
    

就反驳“函子是一个容器”这一直观印象来说，上文定义的 Region 算得上是一个绝佳的反例。在这里，我们用来表示区域的类型是一个函数，与“容器”可谓是风马牛不相及了。

基本上，你在 Swift 中定义的所有泛型枚举都是一个函子。如果能为这些枚举提供一个强大而又熟悉的 map 方法，我们的开发者小伙伴们一定会乐不可支的。

适用函子

除了 map ，许多函子还支持其它的运算。比如第十二章中的解析器，它除了是一个函子之外，还定义了以下运算：

func <*><A, B>(lhs: Parser<(A) -> B>, rhs: Parser<A>) 
        -> Parser<B> {
    

运算符 <*> 将两个解析器顺序化合并：第一个解析器返回一个函数，而第二个解析器为这个函数返回一个参数。对该运算符的选用并非是偶然。对于任意的类型构造体，如果我们可以为其定义恰当的 pure 与 <*> 运算，我们就可以将其称之为一个适用函子 (Applicative Functor)。或者再严谨一些，对任意一个函子 F，如果能支持以下运算，该函子就是一个适用函子：

func pure<A>(_ value: A) -> F<A>
    func <*><A, B>(f: F<A -> B>, x: F<A>) -> F<B>
    

虽然我们并没有为 Parser 定义 pure 运算，但你自己也可以很容易的实现它。实际上，适用函子一直隐藏在本书的各个角落中。比如，上一节定义的 Region 也是一个适用函子：

precedencegroup Apply { associativity: left }
    infix operator <*>: Apply
    
    func pure<A>(_ value: A) -> Region<A> {
        return Region { pos in value }
    }
    
    func <*><A, B>(regionF: Region<(A) -> B>, regionX: Region<A>) -> Region<B> {
        return Region { pos in regionF.value(pos)(regionX.value(pos)) }
    }
    

现在，函数 pure 可以使任意区域都返回某个特定的值。而运算符 <*> 则会将结果区域的参数 Position 分别传入它的两个参数区域，其中一个参数会生成一个类型为 (A) -> B 的函数，另一个则会生成一个类型为 A 的值。接着，合并这两个区域的方法相信你也猜得到，将第一个参数返回的函数应用在第二个参数生成的值上。

许多为 Region 定义的函数都可以借由这两个基础构建模块简短地描述出来。参照第二章中的内容，这里以适用函子的形式编写了一小部分函数作为示例：

func everywhere() -> Region<Bool> {
        return pure(true)
    }
    
    func invert(region: Region<Bool>) -> Region<Bool> {
        return pure(!) <*> region
    }
    
    func intersection(region1: Region<Bool>, region2: Region<Bool>)
        -> Region<Bool>
    {
        let and: (Bool, Bool) -> Bool = { $0 && $1 }
        return pure(curry(and)) <*> region1 <*> region2
    }
    

上述代码展示的，便是利用 Region 类型的适用实例逐个定义区域运算的方式。

适用函子并不仅限于区域和解析器。Swift 内建的可选类型就是适用函子的另一个例子。对应的定义简单明了：

func pure<A>(_ value: A) -> A? {
        return value
    }
    
    func <*><A, B>(optionalTransform: ((A) -> B)?, optionalValue: A?) -> B? {
        guard let transform = optionalTransform,
              let value = optionalValue else { return nil }
        return transform(value)
    }
    

pure 函数将一个值封装在可选值中。由于这个过程通常会被 Swift 做隐式的处理，我们定义的这个版本并不是很实用。而运算符 <*> 就会更有意思一些：传入一个 (可能为 nil 的) 函数和一个 (可能为 nil 的) 参数，它会在两个可选值同时有值时，将函数“适用”在参数上，并将结果返回。如果两个参数中任意一个为 nil，则运算结果也会是 nil。我们也可以为第八章中的 Result 类型定义类似的 pure 与 <*>。

这些定义单独来看并不能发挥什么特别厉害的功效，但组合起来就会很有意思。我们可以回顾一些之前的例子，还能回想起之前的 addOptionals 函数么？一个尝试计算两个可能为 nil 的整数之和的函数：

func addOptionals(optionalX: Int?, optionalY: Int?) -> Int? {
        guard let x = optionalX, y = optionalY else { return nil }
        return x + y
    }
    

利用之前的定义，只需要一条 return 语句，我们就可以定义出一版更为简洁的 addOptionals：

func addOptionals(optionalX: Int?, optionalY: Int?) -> Int? {
        return pure(curry(+)) <*> optionalX <*> optionalY
    }
    

一旦你理解了 <*> 以及类似运算符中所包含的控制流，以上述方式去组织一些复杂的计算就变得轻而易举了。

在可选值章节中还有一个值得回顾的例子：

func populationOfCapital(country: String) -> Int? {
        guard let capital = capitals[country], population = cities[capital]
            else { return nil }
        return population * 1000
    }
    

在这里，我们需要查阅一个字典 capitals，来检索特定国家的首都城市。接着查阅另一个字典 cities 来确定该城市的人口数量。尽管与前例中 addOptionals 的运算过程差不太多，可这个函数却无法以适用的方式来编写。如果我们尝试这样做的话，会发生以下的情况：

func populationOfCapital(country: String) -> Int? {
        return { pop in pop * 1000 } <*> capitals[country] <*> cities[...]
    }
    

这里的问题在于，之前的版本中，第一次查询的结果被绑定在了变量 capital 上，而第二次查询需要调用这个变量。如果只使用适用方式来运算，就会被卡在这里：一个适用运算的结果 (上例中的 capitals[country]) 是无法影响另一个适用运算 (在 cities 中进行查询) 的。要解决这个问题，我们还需要其它的接口。

单子

在第五章中，我们给出了 populationOfCapital 的另一种定义方式：

func populationOfCapital3(country: String) -> Int? {
        return capitals[country].flatMap { capital in
            return cities[capital]
        }.flatMap { population in
            return population * 1000
        }
    }
    

在这里，我们使用了内建的 flatMap 方法来组合可选值的计算过程。这与适用接口的不同点在哪里呢？答案是，类型。在适用运算符 <*> 中，两个参数都是可选值，反观 flatMap 方法，第二个参数却是一个返回可选值的函数。也正是因此，我们才得以将第一个字典的检索结果传递给第二个字典来进行查阅。

只在适用函数之间进行组合是无法定义出 flatMap 方法的。实际上，flatMap 是单子结构支持的两个函数之一。更通俗地说，如果一个类型构造体 F 定义了下面两个函数，它就是一个单子 (Monad)：

func pure<A>(_ value: A) -> F<A>
    
    func flatMap<A, B>(x: F<A>)(_ f: (A) -> F<B>) -> F<B>
    

flatMap 函数有时会被定义为一个运算符 >>=。鉴于它将第一个参数的计算结果绑定到第二个参数的输入上去，这个运算符也被称为“绑定 (bind)”运算。

除了 Swift 的可选值类型之外，第八章中定义的枚举 Result 也是一个单子。按照这个思路，将一些可能返回 Error 的运算连接在一起就变得可行了。比如，我们可以定义一个用来将一个文件的内容复制到另一个文件的函数，如下例：

func copyFile(sourcePath: String, targetPath: String, encoding: Encoding)
        -> Result<()>
    {
        return readFile(sourcePath, encoding).flatMap { contents in
            writeFile(contents, targetPath, encoding)
        }
    }
    

如果对 readFile 与 writeFile 中任何一个方法的调用失败，一个 Error 就会被抛出。虽然上例不如 Swift 的可选值绑定机制那么好用，但也十分接近了。

除了处理错误之外，单子还有很多其它的用武之地。比如，数组也是一个单子。在标准库中，数组的 flatMap 方法已经被定义了，不过你也可以像这样来实现：

func pure<A>(_ value: A) -> [A] {
        return [value]
    }
    
    extension Array {
        func flatMap<B>(_ f: (Element) -> [B]) -> [B] {
            return map(f).reduce([]) { result, xs in result + xs }
        }
    }
    

我们能从这些定义中得到什么呢？作为一个单子结构，数组提供了一种便利的方式来定义各种各样的可组合函数，又或是解决搜索相关的问题。举个例子，假设我们需要计算两个数组 xs 与 ys 的笛卡尔积。笛卡尔积是一个由多元组组成的新数组，每个多元组的第一部分都从 xs 中抽取，第二部分则从 ys 中抽取。直接使用 for 循环的话，我们可能会这样写：

func cartesianProduct1<A, B>(xs: [A], ys: [B]) -> [(A, B)] {
        var result: [(A, B)] = []
        for x in xs {
            for y in ys {
                result += [(x, y)]
            }
        }
        return result
    }
    

我们现在可以使用 flatMap 替换 for 循环来重写 cartesianProduct：

func cartesianProduct2<A, B>(xs: [A], ys: [B]) -> [(A, B)] {
        return xs.flatMap { x in ys.flatMap { y in [(x, y)] } }
    }
    

方法 flatMap 允许我们从第一个数组 xs 中提取一个元素 x，然后在 ys 中提取一个元素 y。对于每一组 x 与 y，我们都会返回一个数组 [(x, y)]。最后，flatMap 方法会将所有这些数组合并为一个结果集。

尽管这个例子看起来有点勉强，flatMap 方法在数组中还是用很多很重要的应用场景。像是 Haskell 与 Python 这样的语言，会专门提供一些语法糖来定义列表，这被称作列表推导式 (list comprehensions)。这些列表推导式允许你从已经存在的列表中抽取元素并检查这些元素是否符合某些指定的规则。所有列表推导式语法糖都可以脱糖为 map、filter 与 flatMap 的组合。列表推导式与 Swift 中的可选值绑定很相似，只不过它们作用于列表而不是可选值。

讨论

为什么要关注这些概念呢？知道某些类型是不是一个适用函子或一个单子真的重要么？我们觉得，是的。

回忆一下第十二章中的解析器组合算子吧。定义一种合适的方式来使两个解析器顺序解析并不容易：这需要对解析器的工作原理有一些相对深入的了解。在我们的库中，这是必不可少的一个环节，否则，我们连最简单的解析器都写不出来。如果你能发觉我们的解析器被构造为了一个适用函子，你就会意识到之前定义的运算符 <*> 为顺序合并两个解析器提供了最优的解决方案。在寻求如此复杂的定义时，对自定义类型所支持的抽象运算有所了解会很有帮助。

像函子这样的抽象概念，也为我们提供了很重要的词汇。如果你偶然遇到了一个名为 map 的函数，你或许能把这个函数的功能猜个八九不离十。若是没有使用精确的术语来描述类似于函子这样的通用结构的话，你可能就要花时间从各种拍脑门的函数名中发觉，这其实就是个 map 函数。

另外，你也可以在设计自己的 API 时以这些结构作为参考。如果你定义了一个泛型枚举或是结构体，且恰好支持 map 运算。这是你希望暴露给用户的接口吗？你的数据结构是不是也是一个适用函子呢？它是一个单子么？这个操作会做些什么？一旦你熟悉了这些抽象结构，问题就会一个接一个的蹦出来。

尽管在 Swift 中比在 Haskell 中要难一些，但你依旧可以为任意适用函子定义合适的泛型函数。就好像解析器运算符 </> 这样的函数，可以借助适用函数 pure 与 <*> 来定义一般。此外，我们可能会想为解析器以外的其它适用函子重新定义这些函数。若是如此，我们便可以利用这些抽象的结构来编写一些程序，继而在编写过程中接触到一些通用的模式；而这些模式本身，也会在很多场合下派上用场。

在函数式编程的世界中，单子还有一段趣的发展史。最开始，单子是在数学领域里一个被称作范畴论的分支中被发展起来的。其与计算机科学的联系通常被归结为 Moggi (1991) 的发现，随后由 Wadler (1992a; 1992b) 将其发扬光大。从那时起，他们就已经开始在 Haskell 这样的函数式语言中使用单子，并对单子的副作用与 I/O (Peyton Jones 2001) 做了控制。而适用函子虽然首先由 McBride and Paterson (2008) 提出，但在当时，其实已经有了很多已知的范例。关于本章中提到的许多抽象概念之间的关系，可以在 Typeclassopedia (Yorgey 2009) 中找到一篇完整的概述。

尾声

那么，函数式编程到底是什么呢？许多人 (错误地) 认为函数式编程只是使用像 map 与 filter 这样的高阶函数进行编程，这可能有点管中窥豹，只见一斑。

我们在引言中提到过，一段被精心设计的 Swift 函数式程序所应该具有三种特性：模块化、对可变状态的谨慎处理，以及选择合适的类型。而在后续的章节中，这三个概念也被一再地提及。

无论是第三章中的 Filter 类型，还是第二章的 Region，高阶函数都是一柄定义抽象概念的利器。不过，这只是开始，而非全部。我们为 Core Image 库定义的函数式封装提供了一个类型安全且模块化的方法来组织复杂的图像滤镜。而第十一章的生成器和序列则帮助我们对循环迭代进行了抽象。

Swift 先进的类型系统甚至可以在运行代码之前就捕获到许多错误。比如第五章中讲述的可选值类型会对可能为 nil 的值做不可信标记；而泛型不仅使代码复用变得简单，更使得类型安全能够被可靠地执行，这些内容都在第四章中有所提及。在第八章与第九章中介绍的枚举和结构体，则为你在自己的代码中精确地构建数据模型时，提供了基本的构建单元。

引用透明的函数更易于被推导和测试。我们在第六章中实现的 QuickCheck 库展示了使用高阶函数为引用透明的函数生成随机单元测试的方式。第七章则告诉我们，Swift 对于值类型的谨慎处理使我们得以在程序中自由地共享数据，而无需担心那些无心之失或是预料之外的变化。

译者注：“引用透明的函数”指那些不会产生副作用 (side effect)，或者说不会改变程序运行状态和修改函数外变量的函数。纯函数式的函数因为不会对函数外的变量产生作用，因此具有引用透明性。

我们可以汇总以上所有的思路来构建一个强大的特定领域的语言。在第十章中构建的图表库与第十二章中的解析器组合算子都定义了一个小的函数集，它们提供的模块化构建单元，足以为错综复杂的问题组合出可行的解决方案。而第十三章中的最后一个案例研究，则展示了如何将这些特定领域语言应用到一个完整的程序中去。

最后，我们在本书中见到的许多类型都承担着相似的功能。在第十四章中，我们展示了如何将它们分类，也揭示了其彼此间的关联。

拓展阅读

想更好地磨练函数式编程技能，一种方式是学习 Haskell。其实函数式语言还有很多种，比如 F#， OCaml, Standard ML, Scala, 以及 Racket。无论是哪种语言，作为对 Swift 语言的学习补充，都是很不错的选择。然而，Haskell 却是最能够考验编程思想的语言。随着对 Haskell 理解的深入，你编写 Swift 的方式也将会随之改变。

如今，优秀的 Haskell 书籍与课程遍地生花。Graham Hutton 所著的《Programming in Haskell》 (2007) 作为一本优秀的入门教程，可以让你熟悉语言基础。《Learn You a Haskell for Great Good!》是一本囊括了许多高级话题的免费在线读物。《Real World Haskell》中讲解了一些大型的案例研究，以及大量在其它书目中难以见到的技术讲解，内容遍及语言特性，调试与自动化测试。Richard Bird 以他的 “Functional Pearl” 而闻名 —— 这是一些优雅且具有指导性的函数式编程范例，你可以在他的著作 《Pearls of Functional Algorithm Design》 (2010) 以及在线版中看到这些内容。《The Fun of Programming》则集合了 Haskell 中嵌入的领域特定语言，涵盖的领域从金融合约到硬件设计 (Gibbons and de Moor 2003)。

如果你希望学习更多关于泛型编程语言设计的内容，Benjamin Pierce 的《Types and Programming Languages》 (2002) 不失为明智之选。Bob Harper 的《Practical Foundations for Programming Languages》 (2012) 虽然发布较新且更为严谨，可如果你的计算机科学与数学功底不够扎实，可能会觉得像在读天书。

不必觉得对以上资源的涉猎都是必须的，其中绝大部分其实都不是你的菜。不过你需要知道的是，编程语言设计、函数式编程与数学的演进在很大程度上直接影响了 Swift 的设计。

如果你希望继续提高自己的 Swift 技艺 —— 且并不只是函数式的部分 —— 我们已经编写了一整本关于 Swift 进阶主题的书，选题从低级编程到高级抽象均有涉及。

结语

对 Swift 来说，现在是最令人激动的时代。这门语言仍然在蹒跚学步。与 Objective-C 相比，它有许多借鉴于其它已存在的函数式编程语言的全新特性，这预示着我们为 iOS 与 OS X 编写程序的方式将产生颠覆性的变化。

与此同时，Swift 的社区发展尚不明朗。人们会接受这些特性么？又或是写着与 Objective-C 相同的代码，只不过少个分号？时间终会给我们答案。在此，我们仅希望能够通过编写此书，使你对一些函数式编程的概念有所了解。而是否要将本书的内容加以实践，可能要取决于你对 Swift 抱有何种期待。言尽于此，愿我们可以一同续写 Swift 的未来！

参考文献