前言

从表面上来说，这本书围绕如何实现高性能集合类型进行展开。针对同一个简单的问题，我们将提供多种不同的解决方案，并依次对它们进行详细地说明。同时为了不断地挑战性能巅峰，我们会一直走在找寻新方法的探索征途中。

Swift 提供了很多工具来帮助我们表达自己的想法，说句心里话，这本书仅仅只是针对这些工具进行了一个愉快的探索。本书不会告诉你如何创造一个卓越的 iPhone 应用；但是它会教给你一些工具和技术，以帮助你更好地借助 Swift 代码的形式来表达想法。

这本书源于我曾为 dotSwift 2017 大会准备的大量笔记和代码。由于准备的材料过于详实有趣，我无法做到将全部东西融入到一次演讲中，也正因如此，我写了这本书。（你完全不需要为了理解这本书而特意去看我的演讲，不过视频仅有 20 分钟左右，而且 dotSwift 的剪辑工作非常棒，使我几乎摇身一变成了一位像样的讲者。不过我确信，你会爱上我迷人的匈牙利口音！）

本书面向的读者

从表面看，这本书的受众是那些想要自己实现集合类型的人，但切不可以知表不知里，Swift 中存在一些能使它更加独特的语言天赋，事实上本书的内容对于任何一个想要学习这些独特天赋的人来说都是十分有用的。无论是学会使用代数数据类型 (algebraic data type)，亦或是了解如何通过写时复制 (copy-on-write) 的引用计数存储来创建 swifty 的数据类型，都将有助于你在日常开发中成为更好的程序员。

本书假设你已经是有一定经验的 Swift 程序员。不过你完全不需要是 Swift 专家：如果你熟悉基本语法，而且已经写了数千行 Swift 代码，那么你一定能够顺利地理解本书。如果你需要快速上手 Swift，我会强烈推荐另一本 objc.io 的书给你，由 Chris Eidhof、Begemann 和 Airspeed Velocity 所著的 Swift 进阶。这本书可是说是 Apple 的 The Swift Programming Language 的接续，它对 Swift 的特性进行了更深入的挖掘，很好地解释了如何以一种符合语言特性 (或者说：swifty)的方式来使用它们。

译者注：您也可以在 ObjC 中国的网站找到 Swift 进阶一书的中译版本。

本书中几乎所有代码都可以运行在支持 Swift 代码的任意平台上。除了在几个特例中，目前标准库和跨平台基础框架都不支持所需要使用的特性，所以我引入了平台特定的代码用以分别支持 Apple 和 GNU/Linux 平台。另外，本书的代码均在 Xcode 8.3.2 自带的 Swift 3.1 编译器中进行了测试。

书籍更新

随着时间的推进，我随时有可能发布新版本，或是为修复 bug，或是为补充资料，或是跟随 Swift 语言的进化而迭代。届时你将可以从你原来购买本书的页面下载更新。此外，你还可以在那里获取到不同格式的书籍：当前版本支持 EPUB、PDF 和 Xcode playground 三种格式。(只要登录购买该书所使用的账号，你将可以无限期免费下载。)

联系作者

如果你发现任何错误，请在本书的 Github 仓库中提交一个 issue 来帮助我解决它。有其它任何类型的反馈，也随时欢迎在 Twitter 上联络我，账号是 @lorentey。如果你钟爱写邮件，发邮件到 collections@objc.io 也完全没问题。

如何阅读本书

我没有打破常规，所以本书的阅读顺序更倾向于从前至后。假设读者按照正序阅读，会发现书中有不少内容需要与前面的章节参照阅读。话虽然这么说，但按照自己的喜好的顺序来阅读也是可以的。不过答应我，这样做的时候就算感觉并不那么顺畅，也不要惆怅，好吗？

这本书包含大量源码。在 playground 版本的书籍中，几乎所有代码都可以编辑，而且你所做的修改会即时反映出来。你可以通过改动代码来亲身体会所讲述的内容 – 有时候最佳的理解方式正是看一看当你改变它时会发生什么。

比如说，Sequence 上有一个很有用的扩展方法，用于将所有元素乱序重排。那部分代码中有几个 FIXME 注释描述了代码实现存在的问题。不妨尝试修改代码来修复它们！

#if os(macOS) || os(iOS) || os(watchOS) || os(tvOS)
import Darwin // 为了支持 arc4random_uniform()
#elseif os(Linux)
import Glibc // 为了支持 random()
#endif
 
extension Sequence {
public func shuffled() -> [Iterator.Element] {
var contents = Array(self)
for i in 0 ..< contents.count {
#if os(macOS) || os(iOS) || os(watchOS) || os(tvOS)
// FIXME: 数组元素数量超过 2^32 时会挂
let j = Int(arc4random_uniform(UInt32(contents.count)))
#elseif os(Linux)
// FIXME: 这里存在模偏差（modulo bias）的问题。 
// 另外，应该通过调用 `srandom` 来为 `random` 配置随机种子。
let j = random() % contents.count
#endif
if i != j {
swap(&contents[i], &contents[j])
}
}
return contents
}
}

为了说明一段代码被执行之后发生了什么，有时我会展示执行结果。作为例子，让我们来试着运行 shuffled，以证明每次运行都返回了新的随机顺序：

(0 ..< 20).shuffled()

[11, 7, 18, 5, 16, 6, 4, 17, 8, 2, 15, 12, 19, 1, 0, 3, 14, 10, 9, 13]

(0 ..< 20).shuffled()

[6, 0, 8, 1, 7, 14, 17, 16, 9, 19, 3, 13, 11, 15, 18, 12, 2, 4, 10, 5]

(0 ..< 20).shuffled()

[10, 2, 1, 19, 4, 12, 15, 9, 14, 0, 3, 7, 6, 13, 8, 18, 5, 17, 11, 16]

在 playground 版本的书籍中，所有输出结果都会被即时生成，因此你会在每次打开这一页时得到一组不同的乱序数字集。

致谢

如果没有读者们针对早期草稿给出的精彩绝伦的反馈，一定没有这本书的今天。除了我的读者们，我尤其还想要感谢 Chris Eidhof，他花了相当多的时间来审查早期的书稿，提出了很多详尽的反馈意见，使本书最终版得到了质的飞跃。

Ole Begemann 作为本书的技术审查者；没有问题能逃过他滴水不漏地审查。他绝妙的建议使得代码更加简明漂亮，而且他发现了很多就连我自己也从未意识到的令人惊叹的细节。

还因为有了 Natalye Childress 顶级的审校，我那笨拙且凌乱的句子们才得以转化成为一本真正用妥帖的英语写成的书。我绝对不是在夸大她的贡献；她几乎对每一个段落都做出了不少适当的调整。

当然了，书中也许尚存问题，但我绝不允许这一群很棒的人因此而被指责。如有不善，还请唯我是问。

最后我想感谢的是 Floppy，我七岁的比格犬：她总是耐心地听我描述纷繁复杂的技术问题，让我能够提供更好的问题解决方案。谢谢你，我的好孩子！

1 引言

集合类型是 Swift 语言的核心抽象概念之一。标准库中的主要集合类型包括：数组 (array)、集合 (set) 和字典 (dictionary)，从小脚本到大应用，它们被用在几乎所有的 Swift 程序中。Swift 程序员都熟悉它们的具体运作方式，而且它们的存在赋予了这门语言独特的个性。

当我们需要设计一个新的通用集合类型时，效仿标准库已经建立的先例不失为一个好办法。但是单纯遵循 Collection 协议的要求并不够，我们还需要再多做一些额外的工作来让它的行为与标准集合类型相匹配。本质上来说，就是要符合一些Swift 风格的难以捉摸的性质，很难解释如何正确地做到这一切，但它们的缺席会让人痛不欲生。

1.1 写时复制 (copy-on-write) 值语义

不知道是否与你的想法不谋而合，我认为 Swift 集合类型中最重要的特性非写时复制值语义莫属。

从本质上来说，值语义在上下文中意味着每个变量都持有一个值，而且表现得像是拥有独立的复制，所以改变一个变量持有的值并不会修改其它变量的值：

var a = [2, 3, 4]

var b = a

a.insert(1, at: 0)

[1, 2, 3, 4]

[2, 3, 4]

为了实现值语义，上述代码需要在某些时候复制数组的底层存储，以允许两个数组实例拥有不同的元素。对于简单值类型 (像是 Int 或 CGPoint) 来说，整个值直接存储在一个变量中，当初始化一个新变量，或是将新值赋给已经存在的变量时，复制都会自动发生。

然而，将一个数组赋给新变量并不会发生底层存储的复制，这只会创建一个新的引用，它指向同一块在堆上分配的缓冲区，所以该操作将在常数时间内完成。直到指向共享存储的变量中有一个值被更改了 (例如：进行 insert 操作)，这时才会发生真正的复制。不过要注意的是，只有在改变时底层存储是共享的情况下，才会发生复制存储的操作。如果数组对它自身存储所持有的引用是唯一的，那么直接修改存储缓冲区也是安全的。

当我们说 Array 实现了写时复制优化时，我们本质上是在对其操作性能进行一系列相关的保证，从而使它们表现得就像上面描述的一样。

(要注意的是，完整的值语义通常被认为是由一些名字很可怕的抽象概念组成，就像是引用透明 (referential transparency)、外延性 (extensionality) 和确定性 (definiteness)。在某种程度上，Swift 的标准集合违反了每一条。比如说，就算两个集合包含完全相同的元素，一个集合的索引在另一个集合中也并不一定有效。因此，Swift 的集合并不是完全引用透明的。)

1.2 `SortedSet` 协议

在开始之前，我们首先需要确定一个想要解决的课题。目前标准库中缺少一个非常常用的数据结构：有序集合 (sorted set) 类型，这是一个类似 Set 的集合类型，但是要求元素是 Comparable (可比较的)，而非 Hashable (可哈希的)，此外，它的元素保持升序排列。接下来，让我们卯足火力来实现一个这样的集合类型吧！

这本书将始终围绕有序集合问题进行，对于用多种方法构建数据结构来说，无疑这会是一个很好的示范。之后我们将会创造一些独立的解决方案，并 (举例) 说明一些有趣的 Swift 编码技术。

现在，我们来起草一份想要实现的 API 协议作为开始。理想情况下，我们希望创建遵循下述协议的具体类型：

public protocol SortedSet: BidirectionalCollection, SetAlgebra {
associatedtype Element: Comparable
}

有序集合的核心是将多个元素按一定顺序放置，所以实现 BidirectionalCollection 是一个合情合理的需求，这允许从前至后遍历，也允许自后往前遍历。

SetAlgebra 包含所有的常规集合操作，像是 union(_:)、isSuperset(of:)、insert(_:) 和 remove(_:)，以及创建空集合或者包含特定内容的集合的初始化方法。如果我们志在实现产品级的有序集合，那么毫无疑问，没有理由不完整实现该协议。然而，为了让这本书在可控范围内，我们将只实现 SetAlgebra 协议中很小的一部分，包括 contains 和 insert 两个方法，再加上用于创建空集合的无参初始化方法：

public protocol SortedSet: BidirectionalCollection, CustomStringConvertible, CustomPlaygroundQuickLookable {
associatedtype Element: Comparable
 
init()
func contains(_ element: Element) -> Bool
mutating func insert(_ newElement: Element) -> (inserted: Bool, memberAfterInsert: Element)
}

作为放弃完整实现 SetAlgebra 的交换，我们添加了 CustomStringConvertible 和 CustomPlaygroundQuickLookable；这样一来，当我们想要在示例代码和 playground 中显示有序集合的内容时，能够稍微得心应手一些。

我们需要知道的是，BidirectionalCollection 有大约 30 项要求 (像是 startIndex、index(after:)、map 和 lazy)，它们中的大多数有默认实现。在这本书中，我们将聚焦于要求的绝对最小集，包括 startIndex、endIndex、subscript、index(after:)、index(before:)、formIndex(after:)、formIndex(before:) 和 count。大多数情况下，我们只实现这些方法，尽管通常来讲，进行专门的处理能获得更好的性能，但我们还是选择将其它方法保持默认实现的状态。不过有一个例外，因为 forEach 是 contains 的好搭档，所以我们也会专门实现它。

1.3 语义要求

通常，实现一个 Swift 协议意味着不仅要遵循它的明确要求，大多数协议还具有一系列在类型系统中无法表达的附加语义要求。这些要求需要被单独写成文档。SortedSet 协议也不例外，我们期望所有实现都能满足下述的六个性质：

相容元素类型：Iterator.Element 和 Element 必须保持类型一致。如果插入某种类型的元素，集合类型的方法却返回了其他类型的元素，这样的处理并没有任何意义。(截至 Swift 3，我们仍然无法规定这两种类型必须一致。我们本可以简单地使用 Iterator.Element 来替代 Element；不过我选择引入一个新的关联类型，这仅仅是为了让上述函数签名简短一点。)
有序：集合类型中的元素需要时刻保持已排序状态。具体一点说就是：如果在实现了 SortedSet 的 set 中，i 和 j 都是有效的下标索引，那么 i < j 必须与 set[i] < set[j] 等效。(这个例子也暗示了我们，集合没有重复元素。)
值语义：通过一个变量更改 SortedSet 类型的实例时，必须不能影响同类型的任意其他变量。这也就是说，我们需要遵循：类型必须表现得像是每个变量都拥有自己的独一无二的值，完全独立于其它所有变量。
写时复制：复制一个 SortedSet 值到新变量的复杂度应该是 \(O(1)\)。存储可能在不同的 SortedSet 值之间部分或完全共享。当需要满足值语义时，所有更改都必须先检查共享存储，并在合适的时机创建新的复制。因此，当存储被共享的时候，一旦发生改变可能需要较长的时间才能完成整个处理。
特定索引：索引和特定的 SortedSet 实例相关联，它们只保证对于这个特定的实例和它的不可变直接复制是有效的。即使 a 和 b 是包含完全相同元素的同一类型的 SortedSet 实例，a 的索引在 b 中也未必有效。(通常在技术上，这种对真的值语义的放宽是一种无奈之举，似乎很难避免。)
索引失效：任何 SortedSet 的改变都可能导致所有已经存在的索引失效，包括 startIndex 和 endIndex。对于具体实现来说，让所有的索引失效并不总是必要的，但是想这么做也没问题。(这一点并不能算是要求，因为这从根本上来说不可能被违背。这只是一个提醒，让我们铭记在心，集合类型的索引很脆弱，需要谨慎地处理。)

注意，如果你忘记实现任意一个要求，编译器并不会提醒你。但是实现它们是至关重要的，只有这样，使用有序集合的一般代码才能有稳定的行为。

假如我们正在实现一个现实可用，满足生产要求的有序集合，我们完全没有必要实现 SortedSet 协议，而只需简单地定义一个直接实现了所有要求的单一类型即可。然而，我们将编写不止一个有序集合，因此有一个规定了所有要求的协议再好不过了，而且我们可以基于它定义通用扩展。

虽然我们还没有具体实现 SortedSet，但是果断先来定义一个通用扩展又何尝不是一个激动人心的选择呢！

1.4 打印有序集合

提供一个 description 的默认实现能够让我们免去今后设置输出格式的麻烦。由于所有的有序集都是集合类型，我们完全可以使用标准集合类型的方法来打印它们，就像标准库的数组和集合一样，将元素用逗号分隔，并用括号括起来：

extension SortedSet {
public var description: String {
let contents = self.lazy.map { "\($0)" }.joined(separator: ", ")
return "[\(contents)]"
}
}

此外，为 customPlaygroundQuickLook 创建一个默认实现也很有价值，这样我们的集合类型在 playground 中的输出也能稍微优美一些。一眼看上去，默认的 Quick Look 视图很难理解，所以我使用属性字符串 (attributed string)，将 description 的字体设置为等宽字体，并以此来代替原来的视图。

#if os(iOS)
import UIKit
 
extension PlaygroundQuickLook {
public static func monospacedText(_ string: String) -> PlaygroundQuickLook {
let text = NSMutableAttributedString(string: string)
let range = NSRange(location: 0, length: text.length)
let style = NSParagraphStyle.default.mutableCopy() as! NSMutableParagraphStyle
style.lineSpacing = 0
style.alignment = .left
style.maximumLineHeight = 17
text.addAttribute(NSFontAttributeName, value: UIFont(name: "Menlo", size: 13)!, range: range)
text.addAttribute(NSParagraphStyleAttributeName, value: style, range: range)
return PlaygroundQuickLook.attributedString(text)
}
}
#endif
 
extension SortedSet {
public var customPlaygroundQuickLook: PlaygroundQuickLook {
#if os(iOS)
return .monospacedText(String(describing: self))
#else
return .text(String(describing: self))
#endif
}
}

2 有序数组 (Sorted Arrays)

想要实现 SortedSet，也许最简单的方法是将集合的元素存储在一个数组中。这引出了一个像下面这样的简单结构的定义：

public struct SortedArray<Element: Comparable>: SortedSet {
fileprivate var storage: [Element] = []
 
public init() {}
}

为了满足协议的要求，我们会时刻保持 storage 数组处于已排序的状态，故此，命其名曰 SortedArray。

2.1 二分查找

为了实现 insert 和 contains，我们需要一个方法，给定一个元素，该方法返回该元素在数组中应当放置的位置。

如何快速实现这样一个方法呢？首先我们需要实现二分查找算法。这个算法的工作原理是，将数组一分为二，舍弃不包含我们正在查找的元素的那一半，将这个过程循环往复，直到减少到只有一个元素为止。下面是 Swift 中实现该算法的方法之一：

extension SortedArray {
func index(for element: Element) -> Int {
var start = 0
var end = storage.count
while start < end {
let middle = start + (end - start) / 2
if element > storage[middle] {
start = middle + 1
}
else {
end = middle
}
}
return start
}
}

值得注意的是，即使我们将集合的元素数量加倍，上述循环也仅仅只需要多进行一次迭代。这可以说是代价相当低了！人们常常说二分查找具有对数复杂度 (logarithmic complexity)，具体来说就是：它的运行时间与数据规模大小大致呈对数比。(用大 O 符号来描述则是：\(O(\log n)\)。)

二分查找是一个巧妙的算法，看似简单，实则暗藏玄机，正确地实现它并不是一件容易的事情。二分查找包含许多索引计算，以至于发生错误的几率并不低，像是差一错误 (off-by-one errors)、溢出问题等等。举个例子：我们运用了表达式 start + (end - start) / 2 来计算中间索引，这看起来似乎有些歪门邪道；通常会更直观地写为 (start + end) / 2。然而，这两个表达式并不总是能够获得相同结果，因为第二个版本的表达式包含的加法运算可能会在集合类型元素数量过多时发生溢出，从而导致运行时错误。

我希望有朝一日二分查找能被纳入 Swift 标准库。在此之前，如果什么时候你需要实现二分查找，务必找一本好的算法书籍作为参考。(尽管我认为这本书也会有一些帮助。) 还有，不要忘记测试你的代码，有时候即使是书中的代码也有 bug！我发现覆盖率 100% 的单元测试能帮助我捕获大多数错误。

我们的 index(for:) 函数所做的事情与 Collection 的标准 index(of:) 方法很相似，不同的是，即使要查找的元素并不存在于当前集合，我们的版本也还是能返回一个有效索引。这个细微但是十分重要的不同点能够让 index(for:) 在插入操作中也相当好用。

2.2 查找方法

提到 index(of:)，我认为借助 index(for:) 来定义它也不失为一个好主意，这样一来它也可以用到更好的算法：

extension SortedArray {
public func index(of element: Element) -> Int? {
let index = self.index(for: element)
guard index < count, storage[index] == element else { return nil }
return index
}
}

Collection 的默认查找算法的原理是：执行一个线性查找来遍历所有元素，直到找到目标或是到达末尾为止。经过我们专门优化后的版本要快得多的多。

检验元素与集合类型的所属关系所需要的代码会稍微少一点，因为我们只需要知道元素是否存在：

extension SortedArray {
public func contains(_ element: Element) -> Bool {
let index = self.index(for: element)
return index < count && storage[index] == element
}
}

实现 forEach 更加容易，因为我们可以直接将这个调用传递给我们的存储数组。数组已经排序，因此这个方法将会以正确的顺序访问元素：

extension SortedArray {
public func forEach(_ body: (Element) throws -> Void) rethrows {
try storage.forEach(body)
}
}

到现在我们已经实现了几个方法，不妨回过头看一看其他 Sequence 和 Collection 的成员，值得开心的是，它们也受益于专门的实现。比如说，由 Comparable 元素组成的序列有一个 sorted() 方法，返回一个包含该序列所有元素的有序数组。对于 SortedArray，简单地返回 storage 就可以实现：

extension SortedArray {
public func sorted() -> [Element] {
return storage
}
}

2.3 插入

向有序集合中插入一个新元素的流程是：首先用 index(for:) 找到它相应的索引，然后检查这个元素是否已经存在。为了维护 SortedSet 不能包含重复元素特性，我们只向 storage 插入目前不存在的元素：

extension SortedArray {
@discardableResult
public mutating func insert(_ newElement: Element) -> (inserted: Bool, memberAfterInsert: Element) 
{
let index = self.index(for: newElement)
if index < count && storage[index] == newElement {
return (false, storage[index])
}
storage.insert(newElement, at: index)
return (true, newElement)
}
}

2.4 实现集合类型

下一步，让我们来实现 BidirectionalCollection。因为我们将所有东西都存储到了一个单一数组中，所以最简单的实现方法是在 SortedArray 和它的 storage 之间共享索引。这样一来，我们可以将大多数集合类型的方法直接传递给 storage 数组，从而大幅度简化我们的实现。

Array 实现的不止是 BidirectionalCollection，实际是有着相同 API 接口但语义要求更严格的 RandomAccessCollection。RandomAccessCollection 要求高效的索引计算，因为我们必须任何时候都能够将索引进行任意数量的偏移，以及测算任意两个索引之间的距离。

一个事实是，我们无论如何都会向 storage 传递各种调用，所以在 SortedArray 上实现相同的协议是一件有意义的事情：

extension SortedArray: RandomAccessCollection {
public typealias Indices = CountableRange<Int>
 
public var startIndex: Int { return storage.startIndex }
public var endIndex: Int { return storage.endIndex }
 
public subscript(index: Int) -> Element { return storage[index] }
}

这样我们就完成了 SortedSet 协议的实现。太棒了！

2.5 例子

让我们来检验一下是否一切正常：

var set = SortedArray<Int>()

for i in (0 ..< 22).shuffled() {

set.insert(2 * i)

}

set

[0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42]

set.contains(42)

true

set.contains(13)

false

看起来不错。但是我们的新集合类型是否具有值语义？

let copy = set

set.insert(13)

set.contains(13)

true

copy.contains(13)

false

看起来答案是肯定的！我们并没有做任何工作来实现值语义；凭借 SortedArray 是一个由单一数组构成的结构体这个仅有的事实，我们得到了前面结果。值语义是一个组合性质，若结构体中的存储属性全都具有值语义，它的行为也会自动表现得一致。

2.6 性能

当我们谈论一个算法的性能时，我们常用所谓的大 O 符号来描述执行时间受输入元素个数的影响所发生的改变，记为：\(O(1)\)、\(O(n)\)、\(O(n^2)\)、\(O(\log n)\)、\(O(n\log n)\) 等。这个符号在数学上有明确的定义，不过你不需要太关注，理解我们在为算法增长率 (growth rate) 分类时使用这个符号作为简写就足够了。当输入元素个数倍增时，一个 \(O(n)\) 的算法会花费不超过两倍的时间，但是一个 \(O(n^2)\) 的算法可能比从前慢四倍，同时一个 \(O(1)\) 的算法的执行时间并不大会受输入影响。

我们可以基于数学来分析我们的算法，合理地推导出渐进复杂度估计值。分析能为我们提供关于性能的有用指标，但它不是绝对的；就其本质而言，由于依赖简化的模型，与真实世界中的实际硬件的行为既有可能相匹配，也有可能存在差池。

为了了解我们的 SortedSet 的真实性能，运行一些性能测试是个好办法。例如，下述代码可以对四个 SortedArray 上的基础操作进行微型性能测试，它们分别是：insert、contains、forEach 和用 for 语句实现的迭代：

func benchmark(count: Int, measure: (String, () -> Void) -> Void) {
var set = SortedArray<Int>()
let input = (0 ..< count).shuffled()
measure("SortedArray.insert") {
for value in input {
set.insert(value)
}
}
 
let lookups = (0 ..< count).shuffled()
measure("SortedArray.contains") {
for element in lookups {
guard set.contains(element) else { fatalError() }
}
}
 
measure("SortedArray.forEach") {
var i = 0
set.forEach { element in
guard element == i else { fatalError() }
i += 1
}
guard i == input.count else { fatalError() }
}
 
measure("SortedArray.for-in") {
var i = 0
for element in set {
guard element == i else { fatalError() }
i += 1
}
guard i == input.count else { fatalError() }
}
}

measure 参数是测量其闭包执行时间的函数，第一个参数表示它的名字。驱动 benchmark 函数的一个简单方法是在不同元素个数的循环中调用它，并打印测量结果：

for size in (0 ..< 20).map({ 1 << $0 }) {
benchmark(size: size) { name, body in 
let start = Date()
body()
let end = Date()
print("\(name), \(size), \(end.timeIntervalSince(start))")
}
}

这是我实际用来画出下面图表时所使用的 Attabench 性能测试框架的简化版。真实的代码中含有更多的测试模板之类的东西，不过实际的测量方式 (measure 闭包中的代码) 并无二致。

绘制我们的性能测试结果，得到图 2.1。注意，在这个图表中，我们对两个坐标轴都使用了对数标度 (logarithmic scales)，这意味着：向右移动一个刻度，输入值的数量翻一倍；向上移动一条水平线，执行时间增长为十倍。

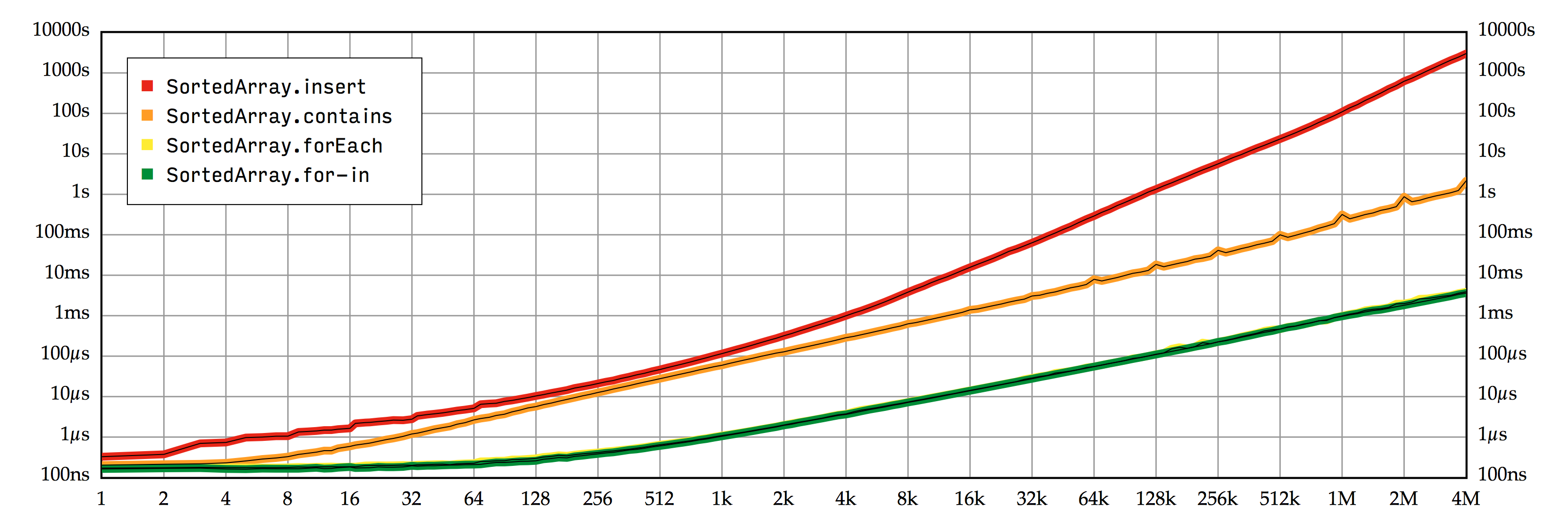
图 2.1: SortedArray 操作的性能测试结果，在双对数坐标系上描画输入值的元素个数和总体执行时间。

双对数坐标系非常适合用来表示性能测试结果。不仅可以无压力地在单一图表上表示跨度巨大的数据，而且有效避免了小值被埋没在大值的世界里。在这个例子中，我们可以很容易地比较元素数量从一增加到四百万的执行时间，尽管它们之间的差异达到了惊人的 22 个二的幂次数量级！

此外，双对数坐标系让我们能够简单地估计一个算法展现的实际复杂度。如果性能测试中某部分是一条直线，那么输入元素个数和执行时间之间的关系近似于一个简单多项式的倍数，如 \(n\)、\(n^2\) 甚至是 \(\sqrt n\)。指数与直线的斜率相关联，\(n^2\) 的斜率是 \(n\) 的两倍。在有了一些亲身实践之后，你会对发生频率最高的关系一目了然，完全没有必要进行复杂的分析。

在我们的例子中，单纯地迭代数组中的所有元素应该会花费 \(O(n)\) 的时间，这在我们的图中也得到了证实。Array.forEach 和 for-in 循环的时间成本几乎相同，而且在初始热身周期之后，它们都变成了直线。横坐标向右移动三个单位多一点，纵坐标就向上移动一个单位，相当于 \(2^{3.3} \approx 10\)，这证明了一个简单的线性关系。

再来看一看 SortedArray.insert 的图，我们会发现元素数量约为 4,000 时它逐渐变化成为一条直线，斜率大致为 SortedArray.forEach 斜率的两倍，由此可以推断插入的执行时间是输入元素数量的二次函数。我们从理论上进行的推测是：每次向已排序数组插入一个随机元素的时候，需要将 (平均) 一半的既有元素向右移动一位来给插入元素腾出位置。因此插入是一个线性操作，\(n\) 个插入操作需要花费 \(O(n^2)\)。很幸运，图表走势与我们的预期相吻合。

SortedArray.contains 进行 \(n\) 次二分查找, 每次花费 \(O(\log n)\) 的时间，因此它应该是一个 \(O(n\log n)\) 的函数。这很难从图 2.1 中看出来, 但是如果你离近了仔细看，便可以验证我们的推测：contains 的曲线几乎平行于 forEach 的曲线，只是稍微向上偏离，但它不是一条完美的直线。你可以将一张纸的边缘放到 contains 图的旁边来进行验证，它弯弯曲曲远离了纸的直边，反映了一种超线性 (superlinear) 关系。

为了突出 \(O(n)\) 和 \(O(n\log n)\) 之间的差异，一个不错的方案是：用输入元素个数除以执行时间，并将结果反映在图表中来展示花费在一个元素上的平均执行时间。(我喜欢把这种类型的图称为平摊图 (amortized chart)。我不确定在上下文中使用平摊合不合适，但是这个词语很容易给人留下深刻的印象！) 这个除法运算排除了斜率始终不变的 \(O(n)\)，使得我们可以简单地区分线性因子和对数因子。图 2.2 展示的是 SortedArray 的平摊图。你会发现，现在 contains 有一个明显 (但是细微) 的向上趋势，而 forEach 的尾部趋于完全水平。

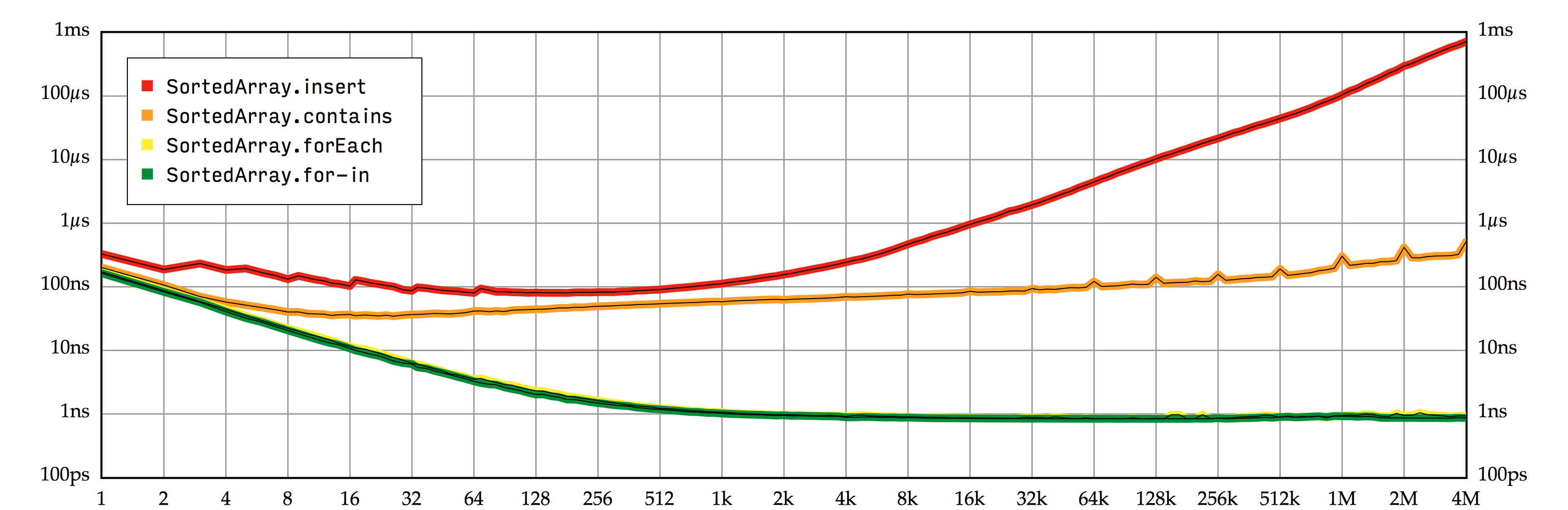
图 2.2: SortedArray 操作的性能测试结果，在双对数坐标系上描画输入值的元素个数和单次操作的平均执行时间。

contains 的曲线带来了两个意料之外的事实。其一是：在元素个数为 2 的幂次方时，会出现一个明显的尖峰。这是因为在二分查找和运行性能测试的 MacBook 的二级 (L2) 缓存架构之间存在一个有意思的相互作用。缓存被分为一些 64 字节的行 (line)，其中每一部分都可能持有来自一系列特定物理地址的内存中的内容。由于一个不幸的巧合，如果存储大小接近于 2 的幂次方时，二分查找算法的连续查找操作可能会落入相同的 L2 缓存行，从而迅速耗尽它的容量，其它行却处于未使用状态。这个现象被称为缓存行别名 (cache line aliasing)，它会导致一个极具戏剧性的性能衰退：contains 峰值耗费的执行时间约为相邻元素个数耗时的两倍。

消除这些尖峰的一种方法是改用三分查找 (ternary search)，每次迭代时将缓存等分为三个部分。还有一种更简单的解决方案，选择一个略微偏离中心的位置作为中心索引来扰乱二分查找。如果选择这个方案，我们只需要在 index(for:) 的实现中修改一行即可，在中心索引上添加一个额外的小偏移量：

let middle = start + (end - start) / 2 + (end - start) >> 6

这样的话，中间索引将落在两个端点的 \(33/64\) 处，足以避免缓存行别名现象。不幸的是，代码变得稍微复杂了一点，相较于二分查找，这些偏离正中的中心索引通常会导致存储查找次数小幅增加。这样看来，消除 2 的幂次方的尖峰所需付出的代价是总体上的衰退，在图表中也得到了证明，如图 2.3 所示。

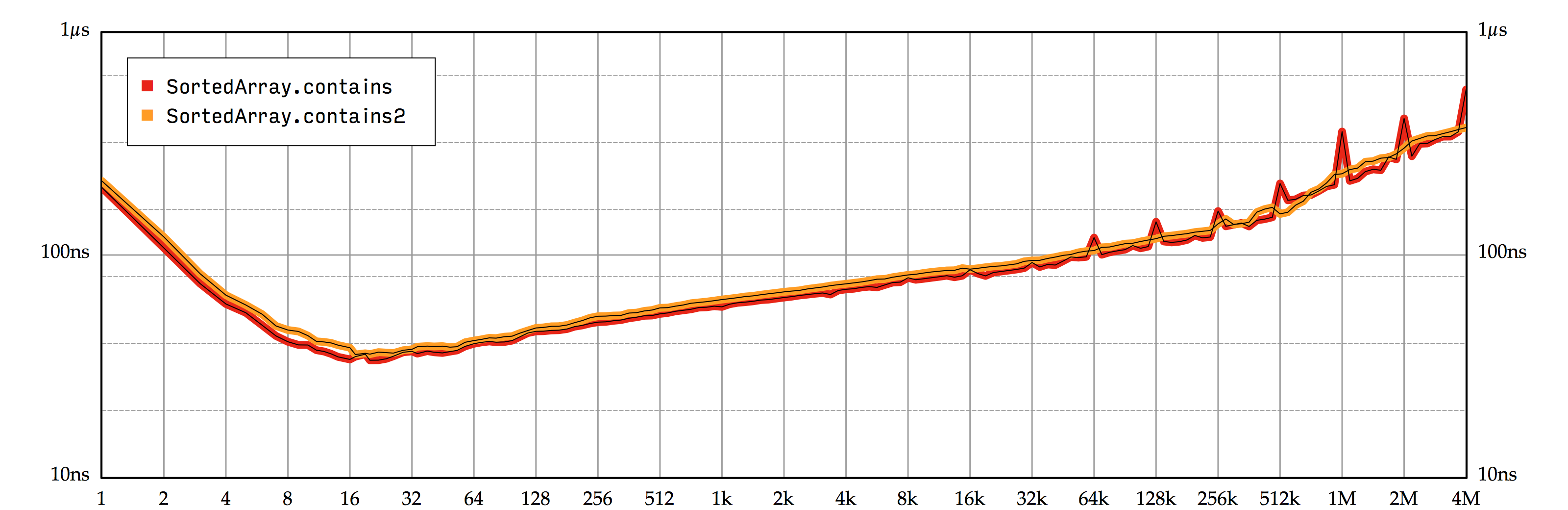
图 2.3: 比较二分查找 (contains) 和使用中心索引偏移来避免缓存行别名的版本 (contains2) 的性能。

还记得上文说的 contains 曲线带来了两个意料之外的事实吗？其二是：在 64,000 个元素及之后，曲线出现轻微上升 (斜率变大)。(如果你仔细观察，你可能会察觉到从大概一百万个元素开始，insert 发生了一个虽然不太明显，但是很类似的衰退。)对于这种规模的元素个数，我的 MacBook 的虚拟内存子系统无法保持 CPU 的地址缓存 (也叫做页表缓存 (Translation Lookaside Buffer)，简称 TLB) 中 storage 数组的所有分页的物理地址。再加上 contains 的性能测试进行的是随机查找，它毫无规律的访问模式导致了 TLB 频繁发生缓存未命中，很大程度上增加了内存访问的成本。另外，随着存储数组的元素个数越来越多，它的绝对大小超过 L1 和 L2 缓存，那些缓存未命中造成了大量附加延迟。

所以在最后，看起来在一个足够大的连续缓冲区进行随机内存访问要花费 \(O(\log n)\) 的时间，而远非 \(O(1)\)，所以我们的二分查找的渐进执行时间实际更像是 \(O(\log n\log n)\)，而非我们通常认为的 \(O(\log n)\)。这结果是不是很有趣？(如果我们从性能测试的代码中将在 lookups 数组上调用的用来随机打乱数组的 shuffled 方法移除，衰退便会烟消云散。试试看！)

另一方面，对于元素个数少的情况，contains 的曲线与 insert 其实非常接近。一部分原因可以归结为对数刻度的副作用，在它们接近的位置，contains 仍然比 insert 快了近 80%。但是 insert 曲线在大约 1,000 个元素时平坦得令人吃惊，似乎当有序数组足够小的时候，插入一个新元素所耗费的时间与数组大小无关。(我认为这是因为在元素个数处于这些区间的时候，整个数组可以完全放入 CPU 的 L1 缓存。)

数组元素足够少的时候，SortedArray.insert 似乎快的难以置信。目前我们可以把这件事视作无关紧要的有趣的假说。但是务必把它牢记在心，因为我们会在本书后面的部分对这个事实进行严肃的讨论。

3 将 `NSOrderedSet` Swift 化

Foundation 框架包含一个名为 NSOrderedSet 的类。它首次于 2012 年登场，与 iOS 5 和 OS X 10.7 Lion 一同诞生，是一个很年轻的类。NSOrderedSet 被添加到 Foundation 中的主要目的是支持 Core Data 中的有序关系。它就像 NSArray 和 NSSet 的合成体一样，同时实现了两个类的 API。正因如此，它提供了 NSSet 中复杂度仅为 \(O(1)\) 的超快成员关系检查和 NSArray 的 \(O(1)\) 复杂度的随机访问索引。作为折中，它继承了 NSArray 的 \(O(n)\) 的插入。由于 NSOrderedSet (算) 是通过封装 NSSet 和 NSArray 实现的，所以相比两者中任意一个，它的内存消耗都要更高一些。

NSOrderedSet 目前还尚未被桥接到 Swift，在这个前提下，尝试为 Objective-C 类定义简单的封装，使其更接近 Swift 的世界，看起来是一个不错的主题。

尽管 NSOrderedSet 是一个很酷的名字，但这与我们的用例并不是十分匹配。NSOrderedSet 的元素的确是有顺序的，不过它并没有强制要求特定的有序关系，你可以以任何喜欢的顺序来进行元素插入，NSOrderedSet 会像一个数组一样为你记住这一切。“ordered” 和 “sorted” 之间的区别在于是否有一个预定义的顺序，这也是为什么 NSOrderedSet 并不能被称为 NSSortedSet 的原因。这么做最根本的目的是让查找操作的速度足够快，不过它使用的实现方法是哈希而非比较。(Foundation 中不存在与 Comparable 协议等效的东西；NSObject 只提供 Equatable (可判等) 和 Hashable (可哈希) 功能。)

但是只要 NSOrderedSet 的元素实现了 Comparable 的话，我们就可以做到保持元素按大小排列，而不仅仅是按插入顺序排列。很明显，对 NSOrderedSet 而言这并不算是理想的使用方式，但是我们确实是可以做到这一点的。接下来就让我们引入 Foundation，开始着手于将 NSOrderedSet 锤炼为 SortedSet：

import Foundation

不过马上我们就遇到了几个大问题。

第一，NSOrderedSet 是一个类，所以它的实例是引用类型。而我们想要让有序集合具有值语义。

第二，NSOrderedSet 是一个混合类型序列，它接受 Any 类型作为成员。实现 SortedSet 时我们依然可以设置它的 Element 类型为 Any，而不是将其作为泛型参数，但是感觉这和我们想要的解决方案还有些差距。我们真正期待的是一个泛型的同质集合类型，它可以通过类型参数来指定其中的元素类型。

基于上述原因，我们不能够只通过扩展 NSOrderedSet 来实现我们的协议。取而代之，我们将会定义一个泛型的封装结构体，它的内部使用 NSOrderedSet 的实例作为存储。这种方法类似于 Swift 标准库为了将 NSArray、NSSet 和 NSDictionary 实例桥接到 Swift 的 Array、 Set 和 Dictionary 值时所做的工作。这样看来，我们似乎步入了正轨。

我们应该给结构体起个什么名字呢？NSSortedSet 这个想法浮现上来，而且在技术上这是可行的，同时 Swift 限定的构造 (现在和将来都) 并不依赖于使用前缀来解决命名冲突。但站在另一方面来看，对于开发者而言，NS 依然暗示着 Apple 提供，所以冒然使用显得很不礼貌，还极容易混淆。我们不妨换个思路，将我们的结构体命名为 OrderedSet。(虽然这个名字也不太正确，但至少像是一个基本数据结构的名字。)

public struct OrderedSet<Element: Comparable>: SortedSet {
fileprivate var storage = NSMutableOrderedSet()
}

我们希望能够修改存储，所以需要将它声明为一个 NSMutableOrderedSet 的实例，NSMutableOrderedSet 是 NSOrderedSet 的可变子类。

3.1 查找元素

现在我们有一个数据结构的空壳。让我们用内容填满它，首先从 forEach 和 contains 这两个查找方法开始。

NSOrderedSet 实现了 Sequence，所以它已经有了一个 forEach 方法。假如元素能够保持正确的顺序，我们可以简单地将 forEach 的调用传递给 storage。然而，我们需要先手动将 NSOrderedSet 提供的值向下转换 (downcast) 为正确类型：

extension OrderedSet {
public func forEach(_ body: (Element) -> Void) {
storage.forEach { body($0 as! Element) }
}
}

OrderedSet 对自身存储具有完全控制权，因此它可以保证存储中永远不会包含除了 Element 以外的任何类型的东西。这确保了向下强制类型转换一定会成功。不过说实话这不太优雅！

NSOrderedSet 恰好也为 contains 提供了实现，而且对于我们的用例来说似乎是完美的。因为不需要显式类型转换，它显得比 forEach 更易于使用：

extension OrderedSet {
public func contains(_ element: Element) -> Bool { 
return storage.contains(element)  // BUG!
}
}

编译上面的代码没有任何警告，当 Element 是 Int 或 String 的时候，它表现得一切正常。但是，正如我们已经提到过的，NSOrderedSet 使用了 NSObject 的哈希 API 来加速元素查找。而我们并未要求 Element 实现 Hashable！这凭什么可以正常工作呢？

当我们像上面的 storage.contains 中做的那样，将一个 Swift 值类型提供给一个接受 Objective-C 对象的方法时，编译器会为此生成一个私有的 NSObject 子类，并将值装箱 (box) 到其中。一定要记住 NSObject 有内建的哈希 API；你不可能有一个不支持 hash 的 NSObject 实例。因此，这些自动生成的桥接类也必然有与 isEqual(:) 一致的 hash 实现。

如果 Element 正好实现了 Hashable，那么 Swift 可以直接在桥接类中使用原类型自己的 == 和 hashValue 实现，这样一来，在 Objective-C 和 Swift 中取得 Element 的值的哈希值就是同样的方法了，而且两者都表现得很完美。

然而，如果 Element 没有实现 hashValue，那么桥接类就只有唯一的选择，那就是使用 NSObject 默认实现的 hash 和 isEqual(_:)。由于没有其它可用信息，它们都将基于实例的标志符 (即物理地址)，而对于被装箱的值类型而言，这是完全随机的。所以两个不同的桥接实例即使持有两个完全相同的值，也不会被认为相等 (或是返回相同的 hash)。

上面的这一切最终使 contains 可以通过编译，但是它却有一个致命的 bug：如果 Element 并未实现 Hashable，则查找总会返回 false。哎呀，糟糕了！

亲爱的，这是一个教训：在 Swift 中使用 Objective-C 的 API 时一定要非常非常小心。将 Swift 值自动桥接到 NSObject 实例确实很便利，但是也存在不易察觉的陷阱。关于这个问题，代码中不会有任何明确的警告：没有感叹号，没有显示转换，什么都没有。

现在我们知道了，在我们的例子中并不能够依赖 NSOrderedSet 的查找方法。所以我们不得不寻找其他 API 来查找元素。谢天谢地，NSOrderedSet 已经包含了另一个查找元素的方法，它依据比较函数的结果对一系列元素进行排序：

class NSOrderedSet: NSObject { // 在 Foundation 中
...
func index(of object: Any, inSortedRange range: NSRange, options: NSBinarySearchingOptions = [], usingComparator: (Any, Any) -> ComparisonResult) -> Int
...
}

我推测这是二分查找某种形式的实现，所以它应该足够快。我们的元素可以根据它们的 Comparable 特性进行排序，因此我们可以使用 Swift 的 < 和 > 操作符来定义一个适合的比较器函数：

extension OrderedSet {
fileprivate static func compare(_ a: Any, _ b: Any) -> ComparisonResult 
{
let a = a as! Element, b = b as! Element
if a < b { return .orderedAscending }
if a > b { return .orderedDescending }
return .orderedSame
}
}

我们可以使用这个比较器来定义一个获取特定元素索引的方法。这正好是 Collection 的 index(of:) 方法应当做的，所以需要确保我们的定义让默认实现更加优雅：

extension OrderedSet {
public func index(of element: Element) -> Int? {
let index = storage.index(
of: element, 
inSortedRange: NSRange(0 ..< storage.count),
usingComparator: OrderedSet.compare)
return index == NSNotFound ? nil : index
}
}

我们有这个函数以后，对 contains 的改造就可以降低到一个很小的范围内：

extension OrderedSet {
public func contains(_ element: Element) -> Bool {
return index(of: element) != nil
}
}

不知道你感觉如何，我发现事情比我预想的要更复杂一些。在如何将值桥接到 Objective-C 的问题上，细节有时会带来深远的影响，这可能会以难以察觉却致命的方法破坏我们的代码。如果我们不知道这些玄机的话，很难不经历意料之外的痛苦。

NSOrderedSet 的 contains 实现特别快，这是它的一个旗舰特性，所以不能够使用 contains 这件事就显得更加悲伤了。但是天无绝人之路！考虑到某些类型下 NSOrderedSet.contains 可能错误地返回 false，但如果值不是确实存在于集合里，它也绝不会返回 true。所以，我们可以写一个新版本的 OrderedSet.contains，依然在其中调用原版本方法，但省去了一部分场景下的二分查找需求：

extension OrderedSet {
public func contains2(_ element: Element) -> Bool {
return storage.contains(element) || index(of: element) != nil
}
}

对于实现了 Hashable 的元素而言，这个版本返回 true 的速度比 index(of:) 更快。不过，遇到值并非集合的成员，或者类型不是可哈希的这两种情况时，处理速度会略微慢一点点。

3.2 实现 `Collection`

NSOrderedSet 只遵循 Sequence，而不遵循 Collection。(这不是什么独特的巧合；它有名的小伙伴 NSArray 和 NSSet 也一样。) 不过，NSOrderedSet 提供了一些基于整数的索引方法，我们可以使用它们在 OrderedSet 中实现 RandomAccessCollection。

extension OrderedSet: RandomAccessCollection {
public typealias Index = Int
public typealias Indices = CountableRange<Int>
 
public var startIndex: Int { return 0 }
public var endIndex: Int { return storage.count }
public subscript(i: Int) -> Element { return storage[i] as! Element }
}

事实证明，这出乎意料的简单。

抱歉，本章其余内容不包含于预览中

请考虑购买本书，或者点击这里了解更多关于本书的内容。

3.3 保证值语义

3.4 插入

3.5 测试

3.6 性能

4 红黑树

自平衡二叉搜索树可以为有序集合类型的实现提供高效的算法。特别是，用这些数据结构来实现的有序集合，其中元素的插入只需消耗对数时间。这实在是一个相当有吸引力的特性，还记得吗，我们实现的 SortedArray 的插入是线性时间复杂度的操作。

“自平衡二叉搜索树”这样的描述看起来多少有些专业，每个词组都有一个具体的含义，之后我会快速地解释一下它们。

树是一种将数据存储在节点内部，按分支排布为树状结构的数据结构。每棵树有一个位于顶部的单独节点，被称作根节点。(树的根被置于顶部，追溯历史，计算机科学家们已经将树颠倒着画了几十年了。这并不是因为他们不知道一棵真实的树长什么样，只不过这样更容易画树形图而已。反正，至少我希望是这样的。) 如果一个节点没有子节点，那就将它称为叶子节点；否则就是一个内部节点。一棵树通常有大量叶子节点。

通常，内部节点可能拥有任意个子节点，但是对于二叉树来说，节点只可以拥有左和右两个子节点。一些节点有两个子节点，当然，只有左子节点或右子节点甚至是根本没有子节点的情况也是时常存在的。

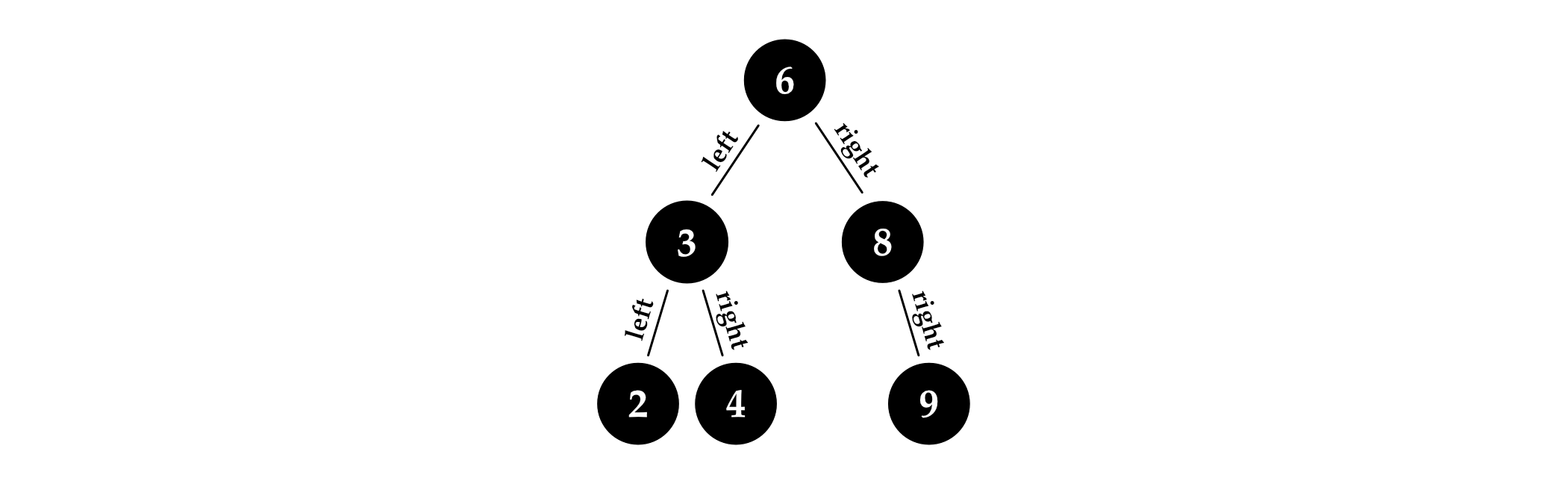
图 4.1: 一棵二分搜索树。节点 6 是根节点；节点 6、3 和 8 是内部节点，而节点 2、4 和 9 是叶子。

在搜索树中，节点内部的值在某种程度上是可比较的，而且树中的节点都是按照一定次序排列的，所有左子树中的值都比节点自身的小，右子树则相反，比节点自身的值更大。这使得查找任意指定元素变得很容易。

通过自平衡 (意味着这个数据结构有排序机制)，无论一棵树包含什么值，以及这些值以什么顺序被插入，这棵树的高度都可以确保尽可能低，且在此范围内保持完整而茂密。如果允许树肆意地生长，那么很简单的操作都可能变得效率奇低。(举一个极端的例子来说，如果一棵树所有的节点最多都只有一个子节点，如同链表一般，那可以说是根本没有效率。)

创建自平衡二叉树的方法有很多；在这个部分中，我们将会实现一个名叫红黑树的版本。由于红黑树自身独有的特征，为了实现自平衡的部分，每个字节都需要额外多存储一位来保存相关信息。这额外的一位是节点的颜色，可以是红色或黑色。

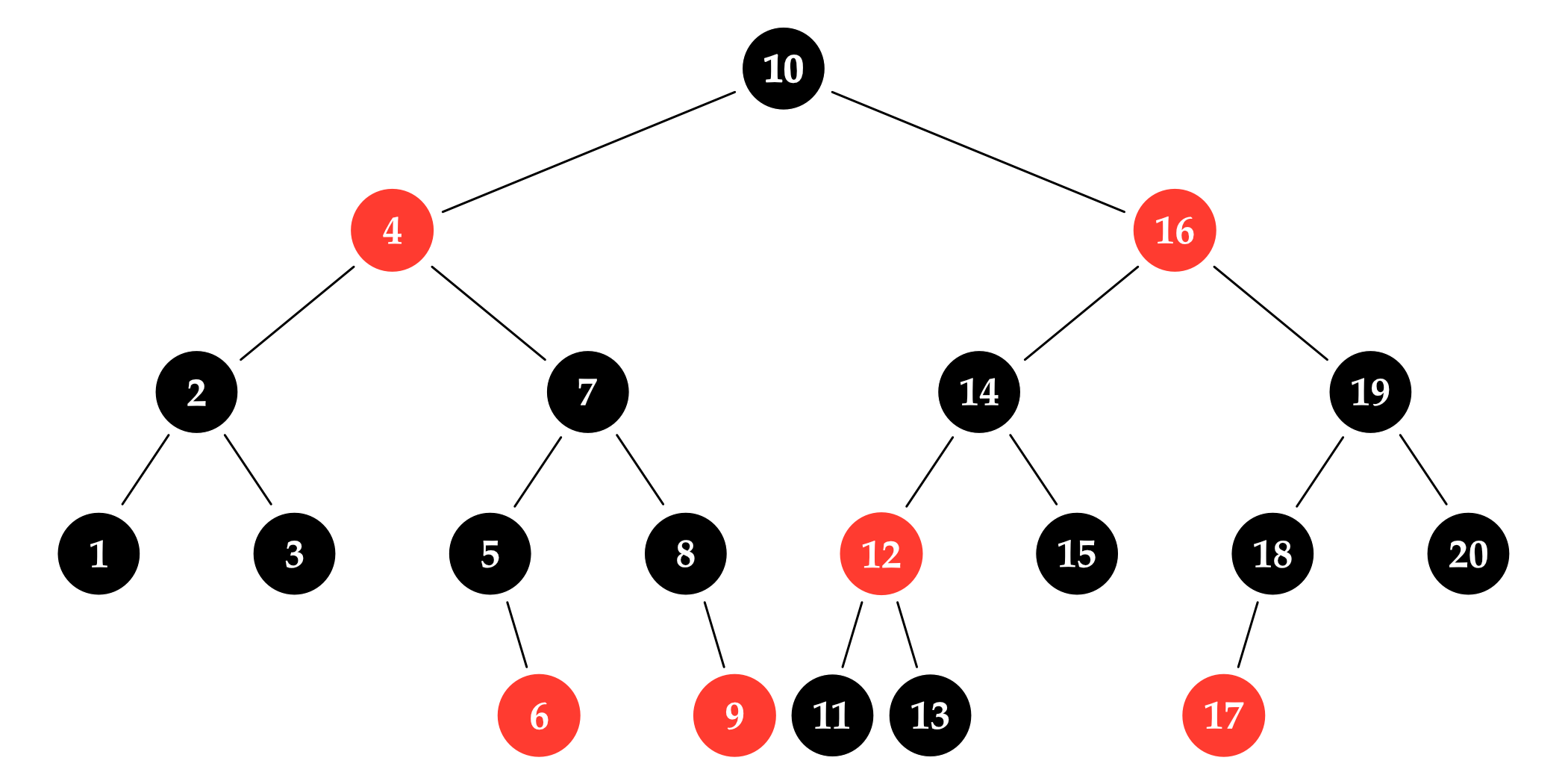
图 4.2: 一棵示例红黑树。

红黑树总是保持它的节点的按照一定顺序排布，并以恰当的颜色着色，从而始终满足下述几条性质：

根节点是黑色的。
红色节点只拥有黑色的子节点。(只要有，就一定是。)
从根节点到一个空位，树中存在的每一条路径都包含相同数量的黑色节点。

空位指的是在树中所有可以插入新节点的空间，即，一个左右子节点都没有的节点。要让增长一个节点，我们只需要用一个新节点替换它的一个空位即可。

第一个性质使得算法略微简单了一点；而且完全不会影响树的形态。后两个性质保证了树的密度始终良好，树中的空位与根节点的距离，不会超过其它任意节点与根节点距离的两倍。

为了完全理解这些平衡性质，稍微做几个小实验，探索一下它们的极端情况，可能会很有帮助。例如，可以构建一棵只包含黑色节点的红黑树；图 4.3 中的树就是一个例子。

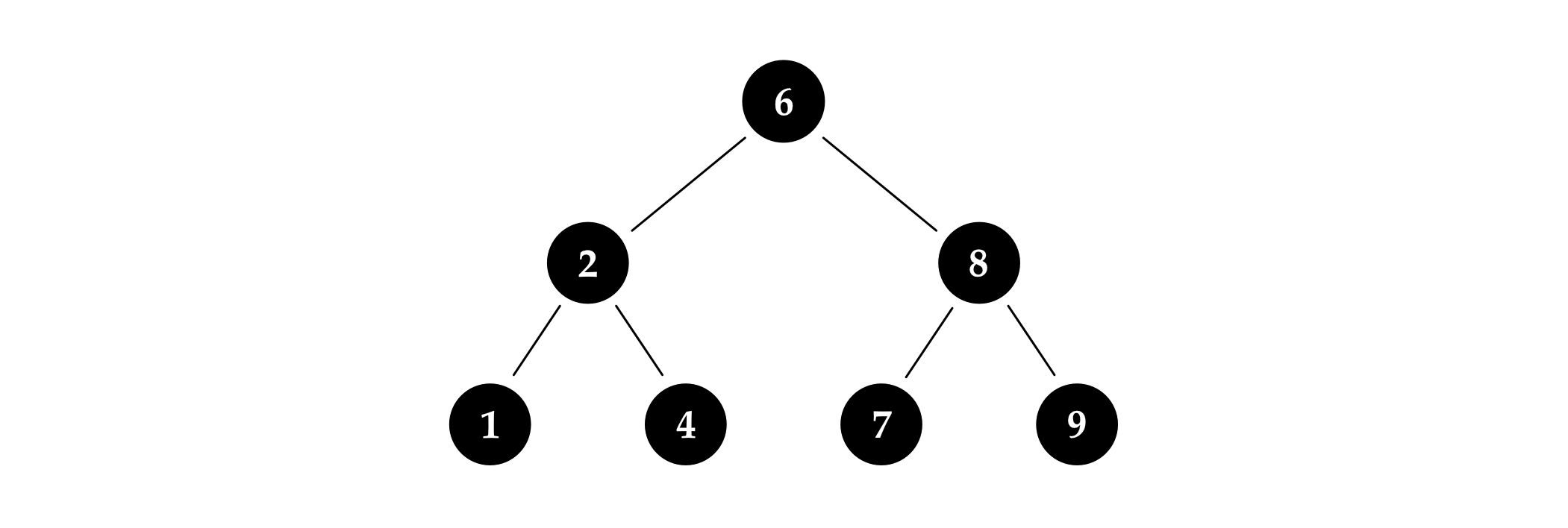
图 4.3: 每个节点都是黑色的示例红黑树。

如果我们尝试构建更多的例子，很快就会意识到红黑树的第三条性质其实将这种树限定为了一种特定的形态：所有内部节点都有两个子节点，而且所有叶子节点都在同一层上。形态如此的树被称为完美树，因为它们完全平衡，完全对称。我们期望所有平衡树都这样生长成这样的理想形态，因为它的每个节点都已尽可能靠近根节点。

不过，要求平衡算法来维护完美树是不可能的：实际上，只有特定的节点数才能构建完美搜索树。比方说，没有哪棵完美树拥有四个节点。

为了使红黑树更实用，第三条性质使用了一个平衡的弱定义，那就是红色节点并不会被计算。不过，为了不让事情变的难以控制，第二条性质将红色节点的数量限制在了合理范围内：这确保了在树中的任何指定路径上，红色节点的数量都不会超过黑色节点。

抱歉，本章其余内容不包含于预览中

请考虑购买本书，或者点击这里了解更多关于本书的内容。

4.1 代数数据类型

4.2 模式匹配和递归

4.3 树形图

4.4 插入

4.5 平衡

4.6 集合类型

4.7 性能

5 写时复制 (Copy-On-Write) 优化

在我们每次向 RedBlackTree 中添加新元素时，都会创建一棵全新的树。新的树会和原来的树共享一些节点，但是在从根节点到新加入的节点的路径上的节点都是新创建的。这种做法可以很“容易”地实现值语义，但是会造成一些浪费。

如果树的某些节点没有被其他值引用的话，我们完全可以直接修改它们。这不会造成任何问题，因为根本没有其他人知道这个特定的树的实例。直接修改可以避免绝大部分的复制和内存申请操作，通常这会让性能得到大幅提升。

Swift 通过提供 isKnownUniquelyReferenced 函数来为引用类型实现优化的写时复制值语义，我们已经介绍过相关内容了。但是在 Swift 3 中，语言本身并没有为我们提供为代数数据类型实现写时复制的工具。我们无法访问 Swift 用来包装节点的私有引用类型，因此也就无法获知某个特定节点是不是只有单一引用。(编译器自己还不够聪明，它也并不能帮我们做写时复制优化。) 同时，想要直接获取一个枚举成员里的值，我们也只能先提取一份它的单独的复制。(注意，与此不同，Optional 通过强制解包运算符 !，提供了直接访问存储的值的方式。然而，为我们自己的枚举类型提供类似的原地访问的工具只能被使用在标准库中，在标准库外它们是不可用的。)

所以，为了实现写时复制，我们现在只能放弃我们钟爱的代数数据结构，将所有东西以一种更“世俗” (或者要我说的话，更乏味) 的命令式的形式进行重写，比如使用传统的结构体和类，以及少量的可选值。

5.1 基本定义

首先，我们需要定义一个公有结构体，用来表示有序集合。下面的 RedBlackTree2 类型是对一个树节点的引用的简单封装，该节点将作为树的存储根节点。这与 OrderedSet 没有任何不同，所以我们现在对这个模式应该已经相当熟悉了：

public struct RedBlackTree2<Element: Comparable>: SortedSet {
fileprivate var root: Node? = nil
 
public init() {}
}

接下来，定义树的节点：

extension RedBlackTree2 {
class Node {
var color: Color
var value: Element
var left: Node? = nil
var right: Node? = nil
var mutationCount: Int64 = 0
 
init(_ color: Color, _ value: Element, _ left: Node?, _ right: Node?) {
self.color = color
self.value = value
self.left = left
self.right = right
}
}
}

在原有的 RedBlackTree.node 枚举成员的基础上，这个类还包含了一个新的属性：mutationCount。它的值表示该节点从被创建以来一共被修改的次数。之后在实现我们的 Collection 时，这个值将被用来构建一种全新的索引方式。(我们这里明确将它定义为 64 位整数，这样就算在 32 位系统中，这个值也不会溢出了。在每个节点中都存储 8 个字节的计数器其实并不太必要，因为我们其实只会使用根节点的这个值。让我们先略过这个细节，这么做能让事情多多少少简单一些，在下一章里我们将会寻找减少浪费的方法。)

不过现在还不是开始说下一章内容的时候！

通过使用不同的类型来代表节点和树，意味着我们可以将节点类型的实现细节隐藏起来，而只将 RedBlackTree2 暴露为 public。对这个集合类型的外部使用者来说，他们将不会把两者混淆起来。在以前，任何人都可以看到 RedBlackTree 的内部实现，都能用 Swift 的枚举字面量语法来创建他们想要的树，这很容易破坏我们的红黑树的特性。

Node 类现在是 RedBlackTree2 结构体的实现细节，将 Node 内嵌在 RedBlackTree2 中很完美地诠释了它们的关系。这也避免了 Node 与同一模块中可能存在的其他同名类型发生命名冲突的问题。同时，这么做还简化了语法：Node 现在将自动继承 RedBlackTree2 的 Element 这一类型参数，我们不再需要明确地进行指定。

同样地，按照传统来说，我们只需要一个 bit 的 color 属性，并将它打包到 Node 的引用属性的二进制表示中某个没有在使用的位即可；但是在 Swift 中这么做既不安全，又很麻烦。我们最好还是简单地将 color 保持为一个独立的存储属性，并且让编译器来设置它的存储。

注意，本质上我们将 RedBlackTree 枚举转换为了 Node 类型的可选值引用。.empty 成员现在以 nil 来表示，而非 nil 的值则表示一个 .node。Node 类型是一个在堆上申请内存的引用类型，所以我们将上一个方案中的隐式打包变成了显式的特性，这让我们可以直接访问堆上的引用，并且可以使用 isKnownUniquelyReferenced。

抱歉，本章其余内容不包含于预览中

请考虑购买本书，或者点击这里了解更多关于本书的内容。

5.2 重写简单的查找方法

5.3 树形图

5.4 实现写时复制

5.5 插入

5.6 实现 `Collection`

5.7 例子

5.8 性能测试

6 B 树

小尺寸 SortedArray 的原生性能看起来几乎不可能挑战。所以我们也就不再争取了，不如另辟蹊径，尝试通过这些高性能的小尺寸有序数组来构建一个有序集合！

一开始非常简单：我们只需要将元素插入到单个数组，直到达到预先规定的元素上限。比如说我们想要将数组的长度保持在四以内，而现在已经插入了四个元素：

如果我们此时需要插入 10，那么数组长度就会超过规定：

我们需要采取一些行动来避免这样的事情发生。一种选择是将数组分割为两半，然后使用中间的那个元素作为两边的分隔元素：

现在，我们有了一个小巧的树形结构，它的叶子节点包含了小尺寸的有序数组。看起来这是一种很有前途的方式：它将有序数组和搜索树合并到了一个统合的数据结构中，这有希望给在小尺寸时给我们带来数组那样超级快的插入操作，同时在大数据集中保持树那样的对数性能。

让我们看看如果继续添加更多元素会发生什么。我们将继续向两个叶子数组中添加新值，直到某一个再次超过范围：

当这种情况发生时，我们需要再进行一次分割，这将给我们带来三个数组以及两个分隔的元素：

对这两个分隔的值，我们应该做些什么呢？我们已经将其他所有元素放在有序数组中了，所以看起来把分隔值也放到它们自己的有序数组里会是个明智的选择：

很显然，新的混合数组树中的每个节点都持有一个小尺寸有序数组。到目前为止，我很喜欢这个想法，它优雅而且一致。

接下来，如果我们想要插入 20 这个值的话，会怎么样呢？它会被放到最右侧的数组中去，不过那里已经有四个元素了，所以我们需要再进行一次分割，将中间值 16 提取出来，成为新的分隔元素。小菜一碟，我们只要将它插入到顶端的数组里就行了：

很好，让我们继续，在插入 25、26 和 27 之后，最右侧的数组又溢出了，于是我们再次提取新的分隔元素，这次是 25:

不过，现在顶端的数组也满了。如果我们接着插入 18、21 和 22，等待我们的便是下面的情况：

接下来怎么办呢？我们可不能放任这个分隔数组就这样膨胀下去。之前，我们通过分割溢出的数组来解决这个问题，这里我们完全可以如法炮制。

哈，完美：通过分割第二层的数组，我们可以在树上添加第三层数组。这让我们可以无限地添加新的元素，当第三层的数组被填满时，我们将添加第四层，以此类推，以至无穷：

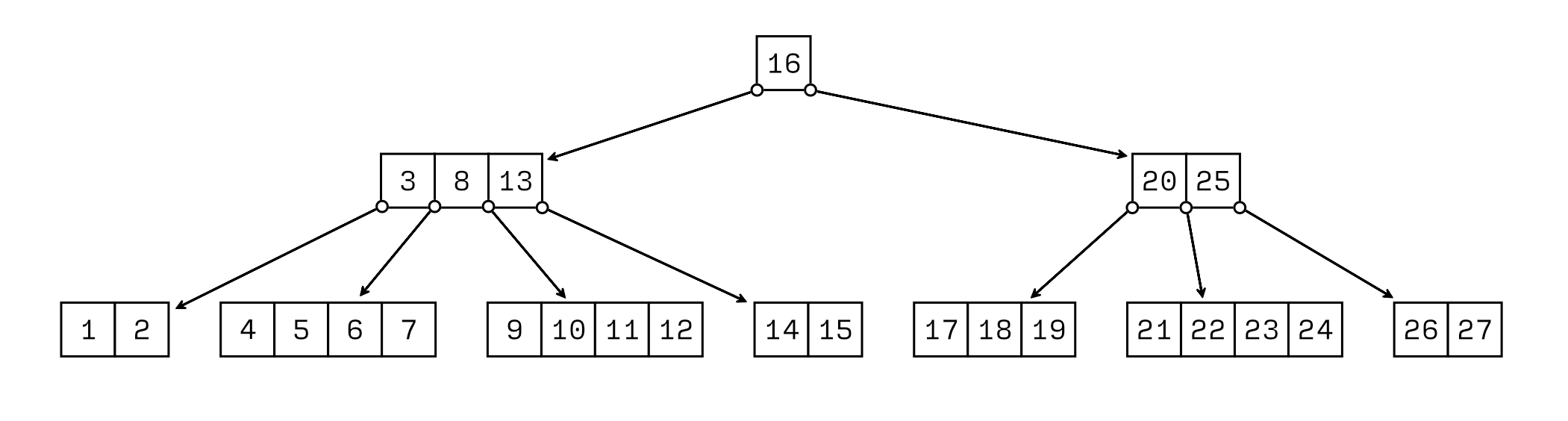
我们刚刚发明了一种全新的数据结构！这是历史性的时刻！

但是高兴得太早了，其实 Rudolf Bayer 和 Ed McCreight 早在 1971 年就提出过一样的想法，他们将这个发明命名为 B 树。真是晴天霹雳，我花了一整本书来介绍一个东西，但是你却告诉我这玩意半个世纪之前就有了，简直悲剧。

有趣的事实是：红黑树实际上是在 1978 年衍生出来的一种 B 树的特殊形式。这些数据结构都经历了岁月的洗礼。

6.1 B 树的特性

正如我们所见，B 树和红黑树一样，都是搜索树，但是它们的结构却有所不同。在 B 树中，节点可能会拥有成百甚至上千的子节点，而不仅仅是两个。不过子节点的个数也并非完全没有限制：节点数肯定会落在某个范围内。

每个节点的最大子节点数在树创建的时候就已经决定了，这个值被叫做 B 树的“阶”。(阶的英文和顺序一样，都是 order，但是阶和元素的顺序无关。) 注意，节点中能存放的元素的最大数量要比它的阶的数字小一。这很可能会导致计算索引时发生差一错误，所以当我们在实现和使用 B 树的时候，一定要将此铭记于心。

在上面，我们构建了一棵阶为 5 的 B 树。实际运用中，阶通常介于 100 到 2,000 之间，5 可以说是小的非同寻常。不过，有 1,000 个子节点的节点没法在页面上表示出来，使用一个能画出来的例子能让我们更容易地理解 B 树。

为了能在树中定位元素，每个内部节点在它的两个子节点之间存储一个元素，这和红黑树中值存储在左右子树之间是类似的。也就是说，一个含有 1,000 个子节点的 B 树节点将存储 999 个按照升序排列好的值。

为了保持查找操作的高效，B 树需要维护如下平衡：

最大尺寸：每个节点最多存储 order - 1 个按照升序排列的元素。
最小尺寸：非根节点中至少要填满一半元素，也就是说，除了根节点以外，其余每个节点中的元素个数至少为 (order - 1) / 2。
深度均匀：所有叶子节点在树中所处的深度必须相同，也就是位于从顶端根节点向下计数的同一层上。

要注意的是，后两个特性是我们的插入方式所诱发的自然结果；我们不需要做任何额外的工作，就可以保证节点不会变得太小，并且所有的叶子都在同一层上。(在其他 B 树操作中，想要维持这些特性会困难的多。比如，删除一个元素可能导致出现不满足要求的节点，此时需要对它进行修正。)

根据这些规则，一个阶为 1,000 的 B 树的节点所能够持有的元素个数在 499 至 999 之间 (包括 999)。唯一的例外是根节点，它不受下限的限制：根节点中可以包含 0 到 999 个元素。(也正因如此，我们才能创建一棵元素个数少于 499 的 B 树。) 这样一来，单独一个 B 树的节点中能够持有的元素个数和一棵 10 到 20 层深的红黑树所能持有的元素个数相当！

将如此之多的元素存放在单个节点中有两个主要好处：

降低内存开销。红黑树中的每个值都存储在一个独立申请于堆上的节点中，该节点还包括了一个指向方法查找表的指针，自身引用计数，以及两个分别指向左右子节点的引用。而 B 树中的节点将批量存储元素，这可以明显地降低内存申请的开销。(具体节省了多少取决于元素个数以及树的阶。)
存取模式更适合内存缓存。 B 树将元素存储在小的连续缓冲区中。如果缓冲区的尺寸经过精心设计，能够全部载入 CPU 的 L1 缓存的话，对它们的操作将会明显快于等效代码对红黑树进行的操作，因为红黑树中的值是散落在堆上的。

为 B 树添加额外的一层，可以使 B 树中所能存储的最大元素个数以阶的乘积的方式增加 (新的最大元素个数 = 原最大个数 × 树的阶)，B 树的稠密特性可见一斑。比如，对于一个阶为 1,000 的 B 树，其最小和最大元素个数随着树的层数的增长情况如下：

Depth	Minimum size	Maximum size
1	0	999
2	999	999 999
3	499 999	999 999 999
4	249 999 999	999 999 999 999
5	124 999 999 999	999 999 999 999 999
6	62 499 999 999 999	999 999 999 999 999 999
⋮	⋮	⋮
\(n\)	\(2 {\left\lceil\frac{order}{2}\right\rceil}^{n-1}-1\)	\(order^{n} - 1\)

很显然，我们几乎不太会有机会处理层级较多的 B 树。理论上，B 树的深度是 \(O(\log n)\)，这里 \(n\) 是元素的个数。但是这个对数的底数实在太大，在真实世界的计算机中，由于可用内存数量的限制，实际上对于任意我们可预期的输入尺寸，可以说 B 树的深度都是 \(O(1)\) 级别的。

最后一句话看起来好像很有道理，而且都这么想的话，会让人觉得是不是只要把时间尺度放大到一个人的剩余生命的话，在实践中所有的算法就都是 \(O(1)\) 复杂度的了。显然，我不会觉得一个跑到我死都没完成的算法是可以“实践”的。不过，你确实能将整个宇宙中可以观测到的粒子都放到一个阶为 1,000 的 B 树中，而这棵 B 树也不过就是 30 多层。所以千万不要去和对数较真，这没什么意义。

在 B 树中，绝大多数元素都是存储在叶子节点中的，这是 B 树如此巨大的扇出 (fan-out) 所导致的另一个有趣的结果。在一个阶为 1,000 的 B 树中，至少 99.8% 的元素存在于叶子节点中。因此，在批量操作 B 树元素 (比如迭代) 时，我们大多数时候需要将注意力放在叶子节点上，对叶子节点进行优化，保持处理迅速：通常，在性能测试的结果中，花在中间节点的时间甚至都不做记录。

奇怪的是，除此之外，B 树的节点数和它的元素数理论上还是成比例的。大多数的 B 树算法和对应的二叉树代码具有相同级别的时间复杂度。不过，在简化后的时间复杂度的背后，实践中复杂度的常数因子也很重要，B 树所做的正是在常数因子上进行优化。不要对此感到意外，因为如果我们完全不关心常数因子的话，这本书在讲完 RedBlackTree 之后就可以终结了！

抱歉，本章其余内容不包含于预览中

请考虑购买本书，或者点击这里了解更多关于本书的内容。

6.2 基本定义

6.3 默认初始化方法

6.4 使用 `forEach` 迭代

6.5 查找方法

6.6 实现写时复制

6.7 谓词工具 (Utility Predicates)

6.8 插入

6.9 实现集合类型

6.10 例子

6.11 性能汇总

7 额外优化

在本章中，我们将集中讨论一下如何进一步优化 BTree.insert，并努力将代码最后的潜力挖掘出来。

我们会创建另外三种 SortedSet 的实现，并“开创性”地将它们命名为 BTree2，BTree3 和 BTree4。为了让本书保持在合理的长度，我们将不会把这三个版本的 B 树的完整代码写出来，只会通过一些具有代表性的代码片段来描述发生的改变。如果你想要参考所有三个版本的 B 树的完整源码，可以去看一看本书的 GitHub 仓库。

如果你已经对 SortedSet 感到厌倦了，跳过本章也没问题。因为这里描述的一些进阶技巧在日常的 app 开发中很少会被用到。

7.1 内联 `Array` 方法

BTree 将元素和 Node 的子节点存储在标准的 Array 中。在上一章里，这使得代码相对容易理解，也对我们认识 B 树起到了帮助。然而，Array 中包含了索引验证和写时复制的逻辑，这和 BTree 中的相关逻辑重复了。如果我们的代码没有任何问题，那么 BTree 将永远不会使用越界的下标访问数组，而且 B 树自己也实现了写时复制的行为。

看看我们的插入性能测试图表 (图 7.1)，可以看到，当集合尺寸相对较小时，虽然 BTree.insert 已经十分接近 SortedArray.insert 了，但它们之间仍然有 10%-20% 的性能差距。消除 Array 的 (微小) 开销是否足以填补这个性能差距？让我们试试看吧！

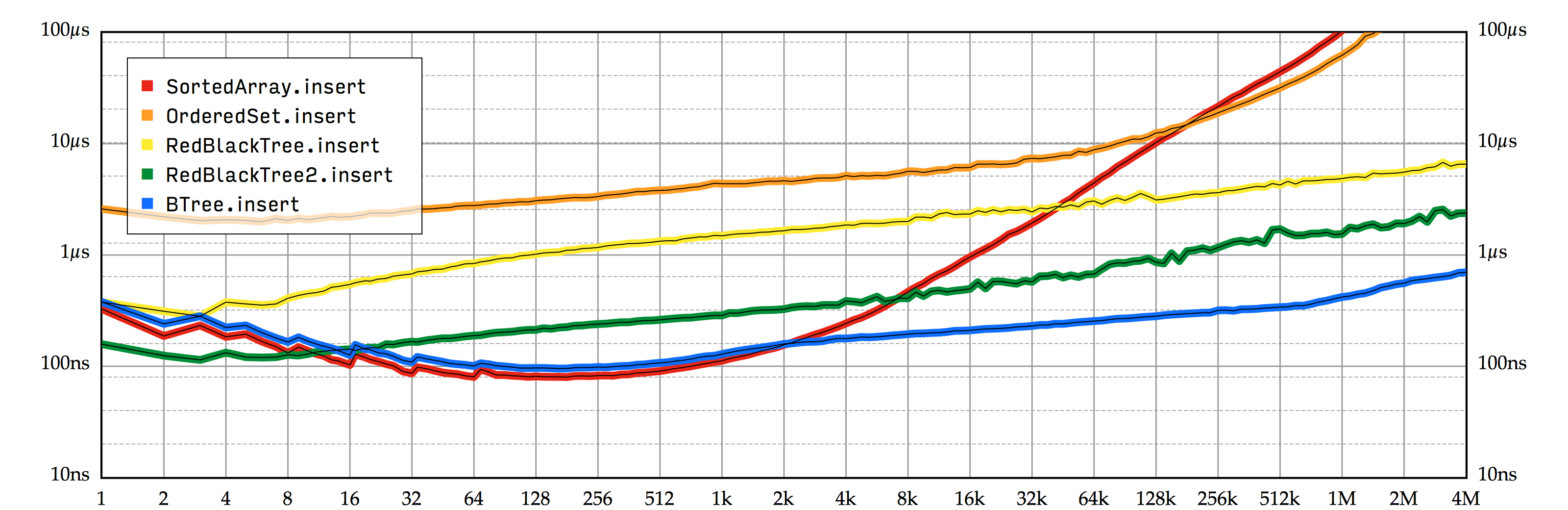
图 7.1: 对比五种不同 SortedSet.insert 实现的性能。

Swift 标准库中包含了 UnsafeMutablePointer 和 UnsafeMutableBufferPointer 类型，我们可以用它们来实现我们自己的存储缓冲区。它们的名字有些可怕，但却名符其实。和这些类型打交道只比和 C 指针打交道好那么一点点，代码上差之毫厘，往往导致结果谬以千里，稍有不慎可能就会造成难以调试的内存污染，内存泄漏，甚至是更糟糕的问题。换个角度来看，如果我们能够细心谨慎地使用这些类型，也许可以通过使用这些类型让我们的性能得到稍许提升。

抱歉，本章其余内容不包含于预览中

请考虑购买本书，或者点击这里了解更多关于本书的内容。

7.2 优化对共享存储的插入

到目前为止，每当测量插入性能时，我们总是假设我们的有序集合的存储是完全独立的。但是我们从没有测试过如果我们将元素插入使用共享存储的集合中时，会发生什么。

为了了解将数据插入共享存储的性能，让我们来设计一种新的性能测量方式吧！一种办法是在每次插入元素后都对整个集合进行复制，然后测量插入一系列元素所花费的时间：

extension SortedSet {
func sharedInsertBenchmark(_ input: [Element]) {
var set = Self()
var copy = set
for value in input {
set.insert(value)
copy = set
}
_ = copy // 避免变量没有被读取的警告。
}
}

图 7.4 展示了对我们到目前为止所实现的 SortedSet 进行这一新的性能测试所得到的结果。

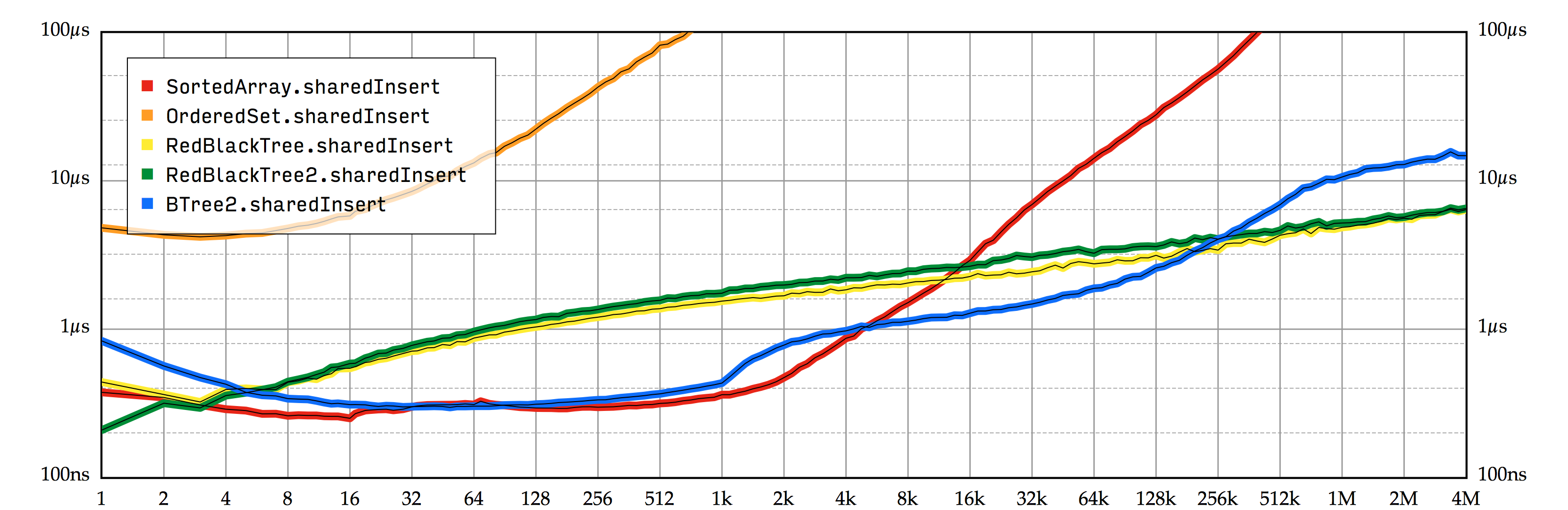
图 7.4: 向共享存储中进行一次插入操作的平摊时间。

显然，我们对 NSOrderedSet 的封装并不是为了针对这种滥用的情况而存在的。一旦元素数量达到几千，它的性能就会比 SortedArray 慢大约一千倍。不过 SortedArray 也没有好多少：为了将存储和复制分离，这两种基于数组的有序集合都需要对存储于其中的每一个值进行完全复制。这不会改变它们的插入操作的渐进性能 (依然是 \(O(n)\) )，但却会为其附加上一个相当可观的常数系数。对 SortedArray 来说，sharedInsert 性能测试要比普通的 insert 慢大约 3.5 倍。

两种红黑树的实现表现得好很多：对于每一次插入操作，它们只需要对落在新插入元素的路径上的节点进行复制。RedBlackTree 不论何时都会这么做：它的插入性能只和节点是否被共享相关。但是 RedBlackTree2 无法使用原地变更：所有的 isKnownUniquelyReferenced 的调用都会返回 false，所以在这个特别的性能测试中，它比 RedBlackTree 要稍微慢一些。

BTree2 最初性能相当好，但是在大约 64,000 个元素时，它突然就变慢了。在这个阶段，树即将增长到三层，它的 (第二层) 根节点中包含了太多的元素，以致于创建一份复制的耗时简直可以和插入操作相提并论。随着树变为三层，这个情况将愈发严重，最后它的性能要比红黑树慢 6 倍左右。(BTree.insert 的平摊性能保持在 \(O(\log n)\)，变慢只是因为添加了一个巨大的常数系数。)

我们希望我们的 B 树在所有图里的速度都遥遥领先于红黑树。那我们能做些什么来防止在共享存储的情况下的这种性能衰退吗？问得好，我们当然有办法！

我们推测，变慢是由于大量的内部节点所导致的。我们也知道，树中绝大部分的值都是存储在叶子节点中的，所以内部节点通常来说并不会对 B 树性能造成很大影响。在这个前提下，我们可以按照我们的想法来任意改造内部节点，而不必担心它会对性能图表产生什么巨大影响。那么，如果我们大幅限制中间节点的最大尺寸，同时保持叶子节点的尺寸不变，会怎么样呢？

要实现这个其实非常简单，我们只需要在 BTree2.insert 中进行一行很小的改动即可：

extension BTree3 {
@discardableResult
public mutating func insert(_ element: Element) -> (inserted: Bool, memberAfterInsert: Element) {
let root = makeRootUnique()
let (old, splinter) = root.insert(element)
if let s = splinter {
let root = BTree3<Element>.Node(order: 16) // <--
root.elementCount = 1
root.elements.initialize(to: s.separator)
root.children = [self.root, s.node]
self.root = root
}
return (inserted: old == nil, memberAfterInsert: old ?? element)
}
}

代码块中被标记出来的一行，为树添加了一个新层。我们用来作为新的根节点的阶的数字，也会被用作所有对它进行分割后所得到的节点的阶数。在这里，通过使用一个小的阶数来代替 self.order，我们确保了所有的内部节点都以这个阶数进行初始化，而不是以原来初始化 BTree 时所用的阶数。(新的叶子节点总是由已存在的叶子节点分割而成，所以这个值不会应用于叶子节点。)

我们将这个新版本的 B 树命名为 BTree3，运行性能测试，可以得到图 7.5 中的结果。上面的推测是正确的；通过限制内部节点的尺寸，性能得到了很大提升！BTree3 现在即使在大数据集的情况下，也比 RedBlackTree 快上 2-2.5 倍。(通过这种费力的方式创建一棵含有四百万个元素的 BTree3 只需要 15 秒；而 BTree2 做同样的事要花 10 倍的时间。)

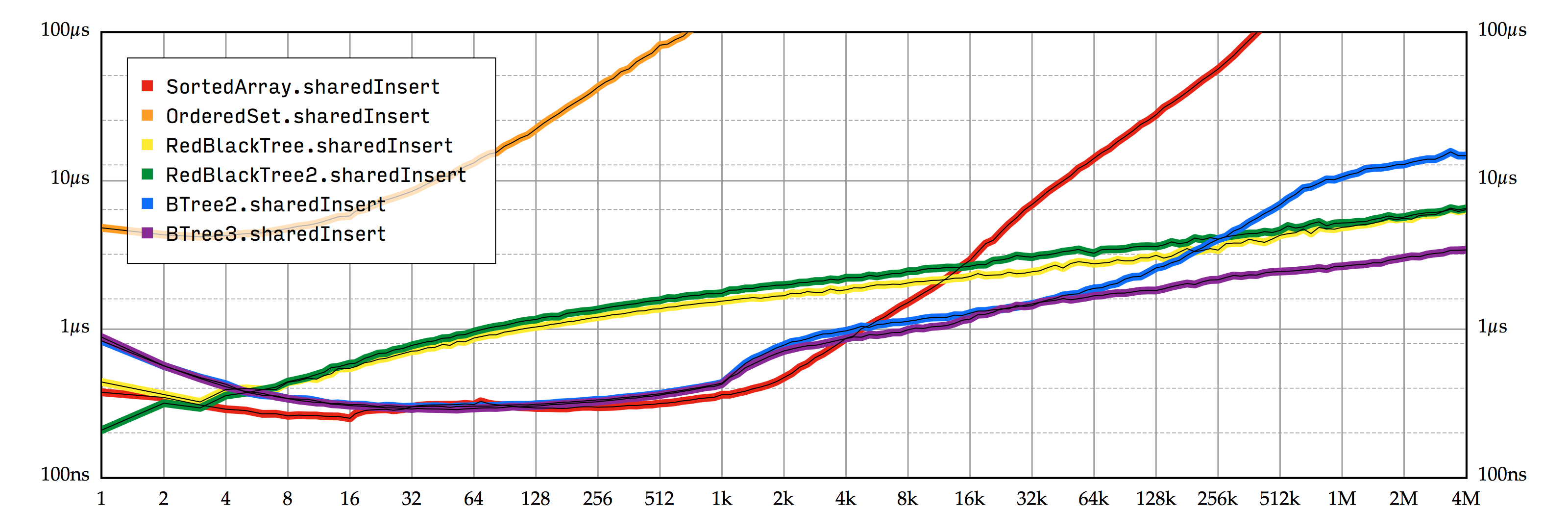
图 7.5: 向共享存储中进行单次插入的平摊时间。

限制内部节点的尺寸通常会增加树的高度，这确实会影响到一部分 B 树的操作。不过，大部分的影响都是可以忽略的：它只会使 contains 和原地的 insert 变慢约 10%，而且它对迭代方法完全没有影响。比如，图 7.6 比较了 BTree3 和我们的其他实现的原地插入操作的性能。

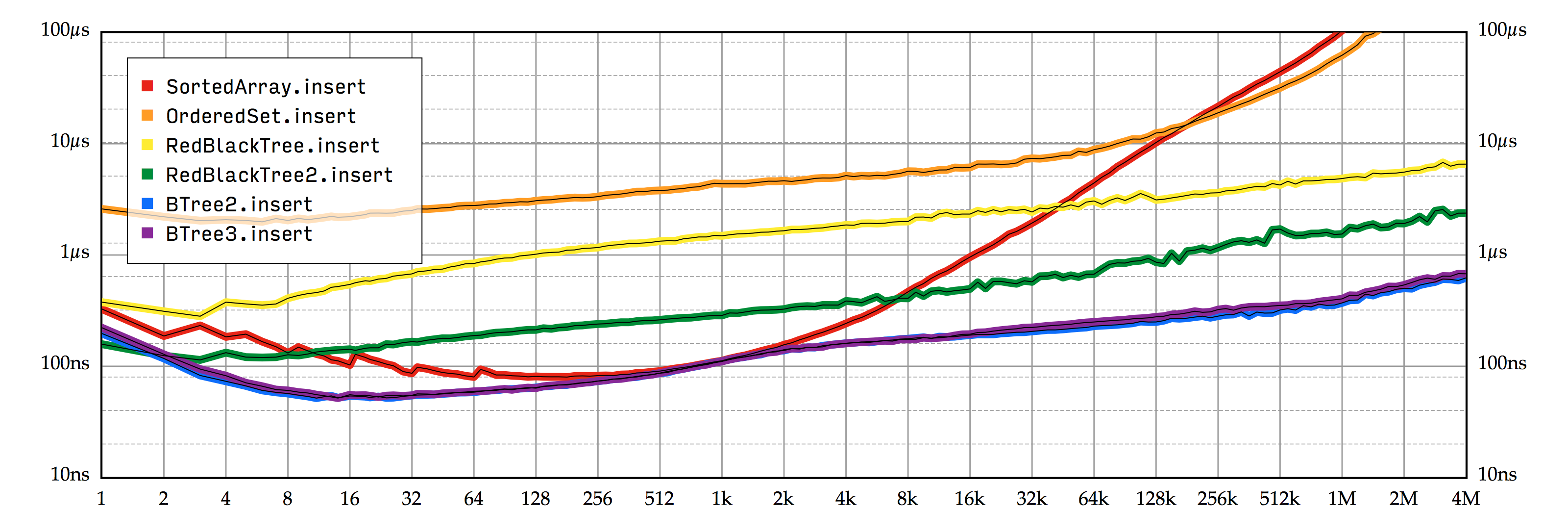
图 7.6: 向共享存储中进行单次插入的平摊时间。

比想象的要简单不少，对吧？

7.3 移除冗余复制

在实现写时复制的时候，我们的代码无一例外地使用了 makeFooUnique 这类方法，以在必要时创建共享存储的复制。之后，我们的代码再分别修改上一步创建的独立存储。

如果你仔细想想，会发现这么做是一种相对不那么有效率的方法：比如，当我们需要在一个共享的 OrderedSet 的开头插入新元素的时候，makeUnique 首先会用完全相同的元素创建一个全新的 NSOrderedSet，然后 insert 立即进行处理，它会把所有的值向右移动一个位置，给新的元素挪出空间。

所以 OrderedSet 的 sharedInsert 测试这么慢就一点都不奇怪了！如果我们在创建共享存储的复制时候已经在正确的位置插入了新元素的话，性能就会得到一定程度的提升。不过我们不会为 OrderedSet 实现这个改进，因为能带来的提升并不多，就算这么做了，与其他的 SortedSet 的实现相比，它的性能还是要差很多。

不过，我们也能从至今为止我们所实现的所有三种 BTree 中看到同样的非最优的行为。当我们向一个共享的 B 树节点插入元素的时候，我们首先会将所有存在的元素复制到新的缓冲区；接下来在一个单独的步骤中插入新的值。更糟糕的是，插入操作还有可能导致节点过大，这时还需要进行分割，将一半的元素移动到第三个缓冲区去，而这件事只能在另一次单独的操作中完成。这么一来，单次的插入操作中，对数百个元素进行复制或移动操作的次数可能不是一次，也不是两次，而是多达三次！这相当低效。

可以通过将 makeUnique、insert 和 split 合并到一个单独的，相对复杂的操作中，从而把所有不必要的复制和移动操作去掉。要将 makeUnique 和 insert 做合并，我们可以实现一个不可变的插入操作，然后，若侦测到节点是共享的，则切换到不可变版本。要将这个混合的插入操作与 split 统一起来，我们需要在插入之前就检测是否需要分割操作。如果需要分割，那么就从头创建两个节点，这样新元素就已经位于正确的位置了。注意，这个新的元素可能会位于第一个节点里，也可能位于第二个节点里，或者甚至正好落在中间，这样的话它就将成为原来节点的两半的分隔值。因此，要将这三种操作统一起来，我们需要写 \(2 \times 4 = 8\) 种独立的插入操作。

我尽自己所能实现了这些方法，但是不幸的是，得到的结果有出有入。共享的插入操作对于特定的元素数量变快了一些，但对于其它的元素数量却又变慢了一些。原地的插入操作没有太大的改变。

这里我不会将我的 BTree4 的代码列在这里，但是你可以在 GitHub 仓库中找到它们。不妨试着调整一下它，也许你可以使它变得更快！

8 总结

在本书中，针对同一个简单的集合类型，我们已经讨论了七种不同的实现方法。每次我们创建一种新的解决方案，我们的代码就变得比之前复杂一些，但是作为交换，我们获取了可观的性能提升。也许用性能测试图表中随着插入实现的进展而稳步下降的曲线最能说明这一点。

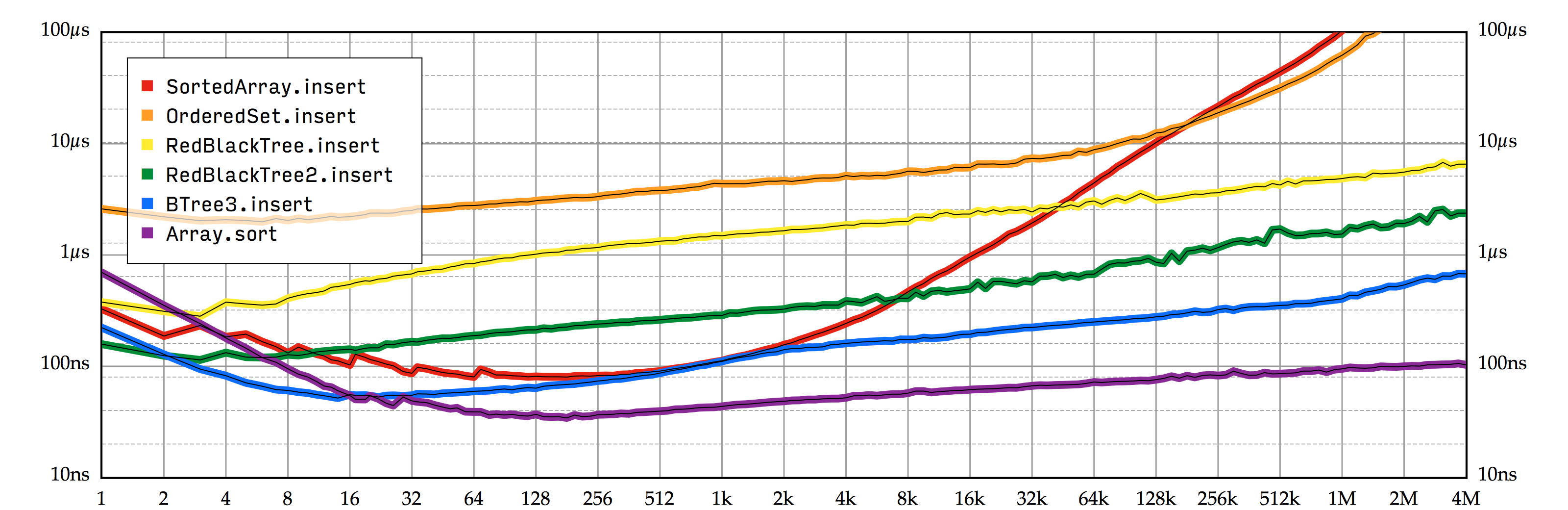
图 8.1: 对比五种 SortedSet 实现的插入性能与 Array.sort 的每个元素的平摊开销。

我们还有可能实现一个更快的 SortedSet.insert 吗？毫无疑问，BTree3 还有一些额外的空间可以进行小幅优化；我想 5-10% 改善完全不是问题。如果我们投入更多努力，甚至有可能可以得到 20% 的提升。

那是否还存在可以给我们带来 200-400% 的巨大性能跳跃的优化手段，而我们又恰恰错过了这些很巧妙的方法呢？我相信答案是没有。

首先要注意，当我们将一系列元素插入到一个有序集合中时，我们实际上是在对它们进行排序。我们可以简单地调用 Array.sort 来做这件事，这个函数使用了超级快的内省排序算法。在上面的图表中，最后一行描述的就是 Array.sort 在每一个元素上所花费的平摊时间。毫无疑问，Array.sort 为我们能够想到的所有有序集合设定了一个性能上限。

在一般尺寸的集合中，通过调用 BTree3.insert 来进行元素排序相较于 Array.sort 仅仅只慢 3.5 倍。这个结果简直接近的让人惊讶！要知道 BTree3 的性能测试是针对每个元素单独处理的，而且每次插入后所有存在的元素依然要保持有序。对于 BTree3.insert 能够在如此不利的条件下还能表现地这么接近，我真是又惊又喜，如果有一种新的 SortedSet 实现能够将 B 树的性能再提升哪怕 50%，我都会觉得大为震惊。

8.1 实现常数时间的插入

虽然可能在保持 BTree3 满足 SortedSet 所有要求的同时，大幅提升性能可能是难以做到的，不过如果我们作点弊的话，我们总归是能让它变得更快的。

比如说，下面代码中的 SillySet 在语法上实现了 SortedSet 协议的要求，而且拥有一个 \(O(1)\) 时间复杂度的 insert 方法。它在上面的 insert 性能测试中不费吹灰之力地就能和 Array.sort 一较高下：

struct SillySet<Element: Hashable & Comparable>: SortedSet, RandomAccessCollection {
typealias Indices = CountableRange<Int>
 
class Storage {
var v: [Element]
var s: Set<Element>
var extras: Set<Element> = []
 
init(_ v: [Element]) { 
self.v = v
self.s = Set(v) 
}
 
func commit() {
guard !extras.isEmpty else { return }
s.formUnion(extras)
v += extras
v.sort()
extras = []
}
}
 
private var storage = Storage([])
 
var startIndex: Int { return 0 }
 
var endIndex: Int { return storage.s.count + storage.extras.count }
 
// 复杂度：`O(n*log(n))`，此处 `n` 是从上一次 `subscript` 被调用以来插入被调用的次数。
subscript(i: Int) -> Element {
storage.commit()
return storage.v[i]
}
 
// 复杂度：O(1)
func contains(_ element: Element) -> Bool {
return storage.s.contains(element) || storage.extras.contains(element)
}
 
// 复杂度：除非存储是共享的，否则为 O(1)
mutating func insert(_ element: Element) -> (inserted: Bool, memberAfterInsert: Element) {
if !isKnownUniquelyReferenced(&storage) {
storage = Storage(storage.v)
}
if let i = storage.s.index(of: element) { return (false, storage.s[i]) }
return storage.extras.insert(element)
}
}

当然了，这里的代码有很多问题：比如，要求 Element 是可哈希的，违反了 Collection 的下标要求，使用 \(O(n \log n)\) 这样慢到令人惊讶的时间复杂度等。但是我认为最让人恼火的是，SillySet 的索引下标带有副作用，它将会改变底层存储，这破坏了 Swift 中我们关于值语义含义的假设。(举个例子，在线程中传递 SillySet 是很危险的，即使是只读的并行访问也会导致数据发生竞争。)

这个特定的例子也许看起来实在是很蠢，不过通过将连续插入操作的值收集起来放到一个单独的缓冲区里，以此推迟实际操作的执行时机这个想法本身还是值得赞赏的。将一系列元素用循环的方式一个个插入到有序集合中，这是一种效率很低的做法。我们可以先将这些元素放到单独的缓冲区中排序，然后在线性时间内用一个特殊的批量加载初始化方法将该缓冲区转为一棵 B 树，这么做的话会快很多。

我们不去关心一个有序集合在插入时的中间状态是否满足要求，因为我们绝不会去使用一个只加载到一半的集合，批量加载之所以可行，正是利用了这一点，我们也因此得到了性能的提升。

辨识这类优化机会是十分重要的，它让我们能暂时脱离一般的限制，而且这会为我们带来在被限制时所不可能得到的大幅度的性能提升。

8.2 再会

我在写这本书的时候获得了很多乐趣，所以我希望您也能喜欢这本书！这一路走来，我学会了不少在 Swift 中实现集合类型的方法，希望您也掌握了一些新的技巧。

在整本书中，我们探索了数种方式，为了解决构建有序集合这一特定问题，我们集中精力对解决方案进行了性能测试，并不断找寻能够改善性能的方式。

不过，这些实现方式都还不完整，我们的代码也并没有真正好到可以在实际产品中使用。为了保持整本书相对较短，我们走了一些捷径，而有些捷径并不适合使用在实际项目之中。

就算是我们的 SortedSet 协议，也是被简化至最小的：我们去掉了 SetAlgebra 中大部分的方法。比如，我们从来没有讨论过如何实现一个 remove 操作。可能你会觉得意外，但事实就是，从一个已经平衡的树中移除元素往往要比添加元素困难得多。(你可以自己试试看！)

我们没有花时间去检查那些我们可以通过平衡搜索树构建的其他数据类型。树结构的有序映射 (map)、列表 (list) ，以及像是多重集合 (multiset) 和多重映射 (multimap) ，都是和有序集合一样重要的数据结构；仔细研究如何改写我们的代码来实现它们会是一件非常有意思的事情。

我们也没有对这些实现方式应当如何被测试做出解释。省略这部分是一个非常艰难的决定，因为我们写了不少取巧的代码，有时候我们甚至使用了不安全的构造方式，最微小的错误都可能会酿成可怕的内存错误，造成让人抓狂的调试工作。

测试实在是太重要了；特别是单元测试，它能为集合类型的正确性提供安全保障，也几乎是进行所有优化工作的先决条件。数据结构自身的特点使它非常适合进行单元测试：它们的操作所接受的输入很容易生成，产生的输出也都是定义良好、易于验证的。使用像是 SwiftCheck 这样强大的工具，可以很容易地为项目提供完整的测试覆盖。

不过，测试写时复制的实现并不是一件简单的事。即使我们不够仔细，不小心在调用 isKnownUniquelyReferenced 之前创建了强引用，我们的代码依然会给出正确的结果，只不过会比我们所期待的慢上许多。我们通常不会在单元测试中检查这样的性能问题，所以我们需要用特殊的手段衡量代码的性能，从而用简单的方法来捕获这类问题。

相反，如果忘记了在改变共享存储前对它进行复制，我们的代码将会影响到那些持有未改变的复制的变量。这样的操作所破坏的值并不一定会明显地表现在操作的输入或者输出上，在原因和结果之间有一定距离的非预期行为是很难被追踪的。就算是我们拥有 100% 的测试覆盖率，一般的输入/输出也不一定会去检测这种情况。因此为了捕获这种错误，我们需要专门为这种情况编写单元测试。

我们简单提到过，通过向一棵搜索树的节点中添加属性来存储节点下的元素个数，我们就可以在 \(O(\log n)\) 的时间内寻找到树中第 \(i\) 个最小或者最大的元素。实际上这个技巧可以被一般化：对包含任意尺度的元素的搜索树，对其进行信息扩充，可以加速所有的关联二分操作。在算法问题中，扩充一直是一个秘密武器：它让我们可以轻易地解决很多看上去复杂的问题。我们这里没有时间对如何实现扩充树以及如何使用它们来解决问题做更详细的解释了。

现在是这本书该完结的时候了，针对我们的问题，我们已经找到了看起来最好的数据结构，此外，我们已经准备好着手将它构建成一个完整的、产品级的解决方案了。从各种角度来说，这都不会是一件简单的工作：我们已经研究过不少操作了，但是仍然需要继续构建和测试更多的代码，并为它们编写文档！

如果你很喜欢本书，并想要亲自动手尝试将集合类型的代码优化为产品可用的质量，可以看看我在 GitHub 上开源的 BTree 项目。在写作时，这个项目最新的版本中甚至还没有包含我们原先在 B 树代码中所做的某些优化，更不用说第七章里的一些进阶内容了。这个项目还有很大的改进空间，我们也随时欢迎您作出贡献。

这本书是如何创建的

本书是由 bookie 生成的，这是一个我用来创建关于 Swift 书籍的工具。(显然 Bookie 是出书人 (bookmaker) 的非正式名字，所以名字上来说我觉得简直是完美契合。)

Bookie 是用 Swift 编写的一个命令行工具，它接受 Markdown 文本文件作为输入，然后生成组织良好的 Xcode Playground、GitHub 样式的 Markdown、EPUB、HTML、LaTeX 以及 PDF 文件，同时它还包括一份含有全部源代码的 Swift 包。Bookie 可以直接生成 playground，Markdown 和源代码，对于其他格式，它将在把文本转换为 Pandoc 自己的 Markdown 方言后再使用 Pandoc 进行生成。

为了验证示例代码，bookie 将会把所有 Swift 代码例子提取到一个特殊的 Swift 包中 (以 #sourceLocation 进行细心标注)，并使用 Swift Package Manager 进行构建。之后得到的命令行 app 将会被运行，所有被用来求值的代码将依次运行，并打印返回值。输出将会被分割，每个独立的结果都将被插回打印版书籍中相应的代码行之后：

func factorial(_ n: Int) -> Int {

return (1 ... max(1, n)).reduce(1, *)

}

factorial(4)

factorial(10)

3628800

(在 playground 中，这些输出是动态生成的；但在其他格式里，输出结果将被包括进来。)

和 Xcode 中一样，语法颜色是通过 SourceKit 完成的。SourceKit 使用的是官方的 Swift 语法，所以上下文关键字总是能够被正确高亮：

var set = Set<Int>() // "set" 也是定义属性 setter 的关键字

set.insert(42)

set.contains(42)

true

本书电子版使用的字体是 Adobe 的思源黑体。示例代码使用的是 Laurenz Brunner 的 Akkurat。

Bookie (暂时还？) 不是一个免费/开源软件，如果你有兴趣在自己的项目中使用它，请直接联系我。

前言

本书面向的读者

书籍更新

相关工作

联系作者

如何阅读本书

致谢

1 引言

1.1 写时复制 (copy-on-write) 值语义

1.2 SortedSet 协议

1.3 语义要求

1.4 打印有序集合

2 有序数组 (Sorted Arrays)

2.1 二分查找

2.2 查找方法

2.3 插入

2.4 实现集合类型

2.5 例子

2.6 性能

3 将 NSOrderedSet Swift 化

3.1 查找元素

3.2 实现 Collection

抱歉，本章其余内容不包含于预览中

3.3 保证值语义

3.4 插入

3.5 测试

3.6 性能

4 红黑树

抱歉，本章其余内容不包含于预览中

4.1 代数数据类型

4.2 模式匹配和递归

4.3 树形图

4.4 插入

4.5 平衡

4.6 集合类型

4.7 性能

5 写时复制 (Copy-On-Write) 优化

5.1 基本定义

抱歉，本章其余内容不包含于预览中

5.2 重写简单的查找方法

5.3 树形图

5.4 实现写时复制

5.5 插入

5.6 实现 Collection

5.7 例子

5.8 性能测试

6 B 树

6.1 B 树的特性

抱歉，本章其余内容不包含于预览中

6.2 基本定义

6.3 默认初始化方法

6.4 使用 forEach 迭代

6.5 查找方法

6.6 实现写时复制

6.7 谓词工具 (Utility Predicates)

6.8 插入

6.9 实现集合类型

6.10 例子

6.11 性能汇总

7 额外优化

7.1 内联 Array 方法

抱歉，本章其余内容不包含于预览中

7.2 优化对共享存储的插入

7.3 移除冗余复制

8 总结

8.1 实现常数时间的插入

8.2 再会

这本书是如何创建的

1.2 `SortedSet` 协议

3 将 `NSOrderedSet` Swift 化

3.2 实现 `Collection`

5.6 实现 `Collection`

6.4 使用 `forEach` 迭代

7.1 内联 `Array` 方法